Question Number 19150 by Tinkutara last updated on 06/Aug/17

Commented by Tinkutara last updated on 06/Aug/17
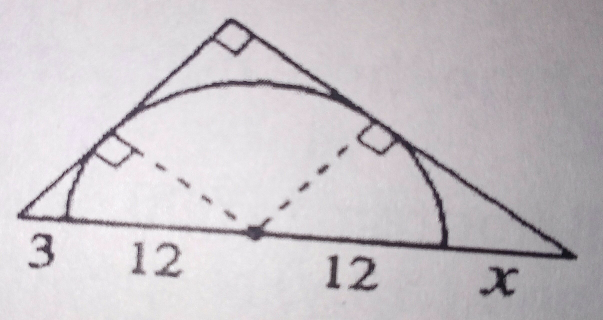
Commented by ajfour last updated on 06/Aug/17

Commented by ajfour last updated on 06/Aug/17
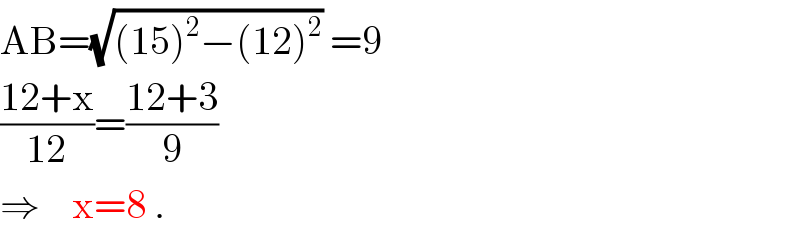
Commented by Tinkutara last updated on 06/Aug/17
Answered by sandy_suhendra last updated on 06/Aug/17
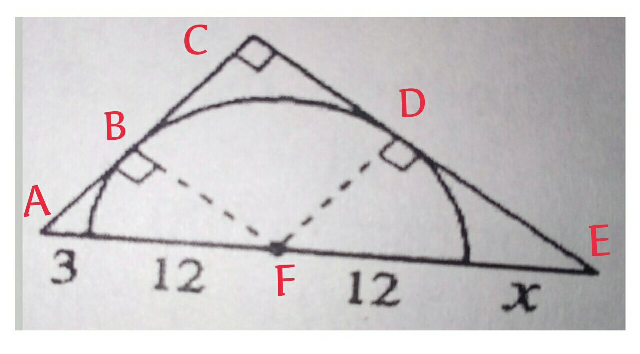
Commented by allizzwell23 last updated on 06/Aug/17

Commented by sandy_suhendra last updated on 06/Aug/17

Commented by Tinkutara last updated on 06/Aug/17