Question Number 129337 by TITA last updated on 15/Jan/21
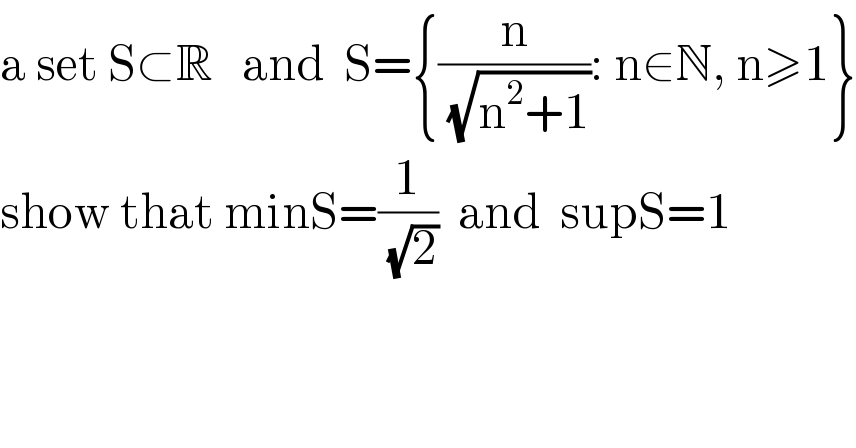
$$\mathrm{a}\:\mathrm{set}\:\mathrm{S}\subset\mathbb{R}\:\:\:\mathrm{and}\:\:\mathrm{S}=\left\{\frac{\mathrm{n}}{\:\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}}:\:\mathrm{n}\in\mathbb{N},\:\mathrm{n}\geqslant\mathrm{1}\right\} \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{minS}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\:\mathrm{and}\:\:\mathrm{supS}=\mathrm{1} \\ $$
Commented by TITA last updated on 15/Jan/21

$$\mathrm{please}\:\mathrm{help} \\ $$
