Menu Close

A-sonometer-wire-60cm-long-under-a-tension-of-120N-vibrates-in-unison-with-a-turning-fork-of-frequency-512Hz-The-wire-is-then-shortened-by-2cm-the-tension-remaining-the-same-If-the-fork-and-wire-are-s

Tinku Tara 0 Comments
Pin




Question Number 35878 by NECx last updated on 25/May/18
A sonometer wire 60cm long,under a tension of 120N,vibrates in unison with a turning fork of frequency 512Hz.The wire is then shortened by 2cm,the tension remaining the same.If the fork and wire are sounded together,how many beats per second are heard? What decrease in tension will be required to restore the frequency of vibration of the wire to the original value?
$${A}\:{sonometer}\:{wire}\:\mathrm{60}{cm}\:{long},{under} \\ $$$${a}\:{tension}\:{of}\:\mathrm{120}{N},{vibrates}\:{in} \\ $$$${unison}\:{with}\:{a}\:{turning}\:{fork}\:{of} \\ $$$${frequency}\:\mathrm{512}{Hz}.{The}\:{wire}\:{is}\:{then} \\ $$$${shortened}\:{by}\:\mathrm{2}{cm},{the}\:{tension} \\ $$$${remaining}\:{the}\:{same}.{If}\:{the}\:{fork} \\ $$$${and}\:{wire}\:{are}\:{sounded}\:{together},{how} \\ $$$${many}\:{beats}\:{per}\:{second}\:{are}\:{heard}? \\ $$$${What}\:{decrease}\:{in}\:{tension}\:{will}\:{be} \\ $$$${required}\:{to}\:{restore}\:{the}\:{frequency} \\ $$$${of}\:{vibration}\:{of}\:{the}\:{wire}\:{to}\:{the} \\ $$$${original}\:{value}? \\ $$
Commented by NECx last updated on 28/May/18
somebody please help
$${somebody}\:{please}\:{help} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/May/18
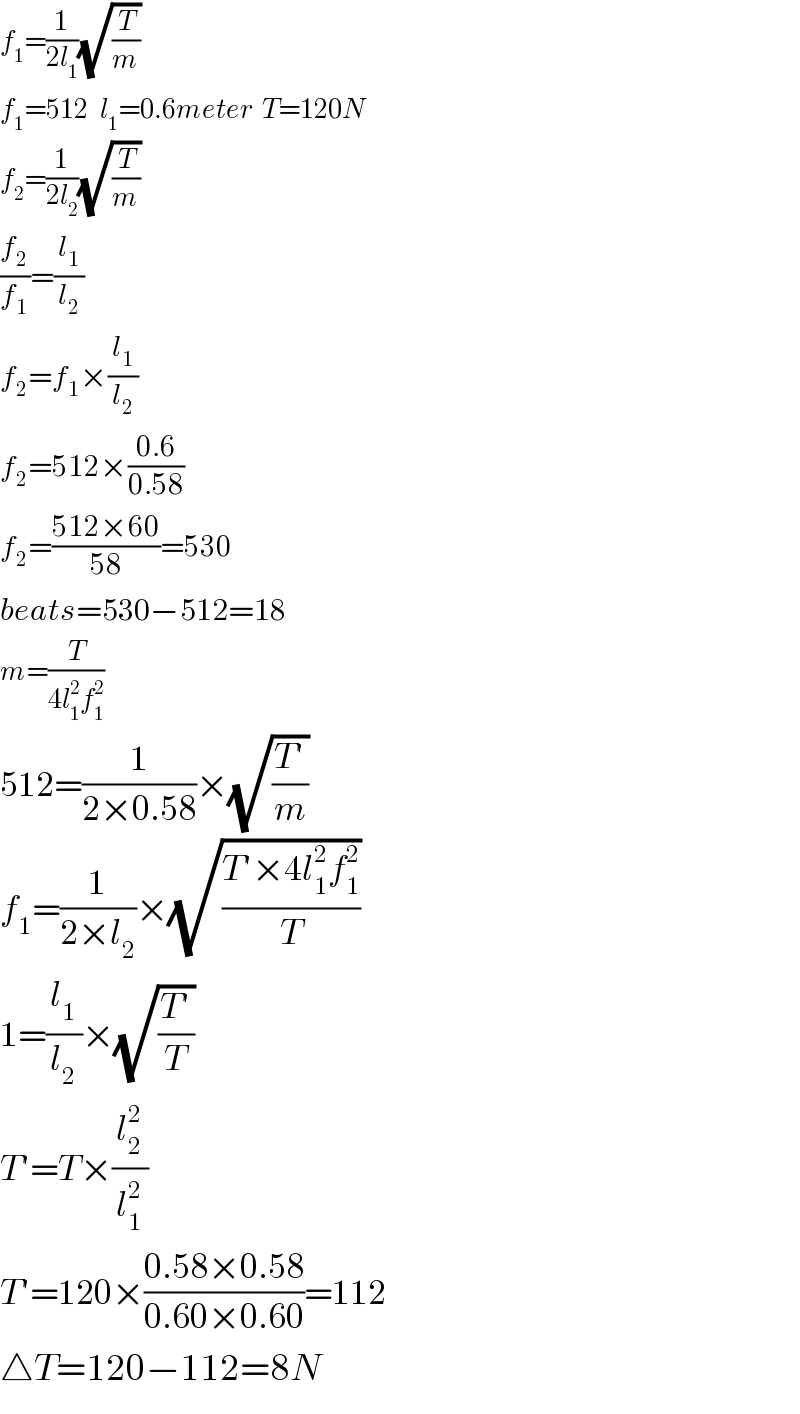
f_1 =(1/(2l_1 ))(√(T/m)) f_1 =512 l_1 =0.6meter T=120N f_2 =(1/(2l_2 ))(√(T/m)) (f_2 /f_1 )=(l_1 /l_2 ) f_2 =f_1 ×(l_1 /l_2 ) f_2 =512×((0.6)/(0.58)) f_2 =((512×60)/(58))=530 beats=530−512=18 m=(T/(4l_1 ^2 f_1 ^2 )) 512=(1/(2×0.58))×(√((T′)/m)) f_1 =(1/(2×l_2 ))×(√((T′×4l_1 ^2 f_1 ^2 )/T)) 1=(l_1 /l_2 )×(√((T′)/T)) T′=T×(l_2 ^2 /l_1 ^2 ) T′=120×((0.58×0.58)/(0.60×0.60))=112 △T=120−112=8N
$${f}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}{l}_{\mathrm{1}} }\sqrt{\frac{{T}}{{m}}} \\ $$$${f}_{\mathrm{1}} =\mathrm{512}\:\:\:{l}_{\mathrm{1}} =\mathrm{0}.\mathrm{6}{meter}\:\:{T}=\mathrm{120}{N} \\ $$$${f}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}{l}_{\mathrm{2}} }\sqrt{\frac{{T}}{{m}}} \\ $$$$\frac{{f}_{\mathrm{2}} }{{f}_{\mathrm{1}} }=\frac{{l}_{\mathrm{1}} }{{l}_{\mathrm{2}} } \\ $$$${f}_{\mathrm{2}} ={f}_{\mathrm{1}} ×\frac{{l}_{\mathrm{1}} }{{l}_{\mathrm{2}} } \\ $$$${f}_{\mathrm{2}} =\mathrm{512}×\frac{\mathrm{0}.\mathrm{6}}{\mathrm{0}.\mathrm{58}} \\ $$$${f}_{\mathrm{2}} =\frac{\mathrm{512}×\mathrm{60}}{\mathrm{58}}=\mathrm{530} \\ $$$${beats}=\mathrm{530}−\mathrm{512}=\mathrm{18} \\ $$$${m}=\frac{{T}}{\mathrm{4}{l}_{\mathrm{1}} ^{\mathrm{2}} {f}_{\mathrm{1}} ^{\mathrm{2}} } \\ $$$$\mathrm{512}=\frac{\mathrm{1}}{\mathrm{2}×\mathrm{0}.\mathrm{58}}×\sqrt{\frac{{T}'}{{m}}} \\ $$$${f}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}×{l}_{\mathrm{2}} }×\sqrt{\frac{{T}'×\mathrm{4}{l}_{\mathrm{1}} ^{\mathrm{2}} {f}_{\mathrm{1}} ^{\mathrm{2}} }{{T}}} \\ $$$$\mathrm{1}=\frac{{l}_{\mathrm{1}} }{{l}_{\mathrm{2}} }×\sqrt{\frac{{T}'}{{T}}} \\ $$$${T}'={T}×\frac{{l}_{\mathrm{2}} ^{\mathrm{2}} }{{l}_{\mathrm{1}} ^{\mathrm{2}} } \\ $$$${T}'=\mathrm{120}×\frac{\mathrm{0}.\mathrm{58}×\mathrm{0}.\mathrm{58}}{\mathrm{0}.\mathrm{60}×\mathrm{0}.\mathrm{60}}=\mathrm{112} \\ $$$$\bigtriangleup{T}=\mathrm{120}−\mathrm{112}=\mathrm{8}{N} \\ $$
Commented by NECx last updated on 29/May/18
wow..... Thanks mr Tanmay.
$${wow}…..\:{Thanks}\:{mr}\:{Tanmay}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *