Question Number 13636 by chux last updated on 21/May/17

$$\mathrm{A}\:\mathrm{steam}\:\mathrm{envine}\:\mathrm{of}\:\mathrm{efficiency}\:\mathrm{70\%} \\ $$$$\mathrm{burns}\:\mathrm{20g}\:\mathrm{of}\:\mathrm{coal}\:\mathrm{to}\:\mathrm{produce}\:\mathrm{10kJ} \\ $$$$\mathrm{of}\:\mathrm{energy}.\mathrm{If}\:\mathrm{it}\:\mathrm{burns}\:\mathrm{200g}\:\mathrm{of}\:\mathrm{coal}\: \\ $$$$\mathrm{per}\:\mathrm{second},\mathrm{calculate}\:\mathrm{its}\:\mathrm{output} \\ $$$$\mathrm{power}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by ajfour last updated on 21/May/17
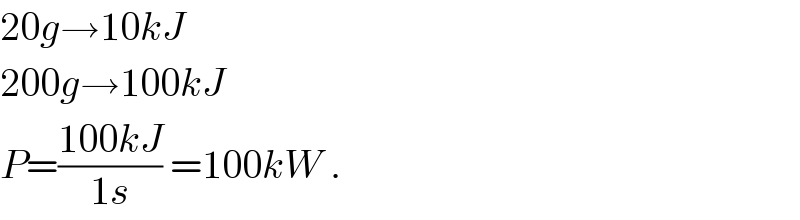
$$\mathrm{20}{g}\rightarrow\mathrm{10}{kJ} \\ $$$$\mathrm{200}{g}\rightarrow\mathrm{100}{kJ} \\ $$$${P}=\frac{\mathrm{100}{kJ}}{\mathrm{1}{s}}\:=\mathrm{100}{kW}\:. \\ $$
Commented by chux last updated on 21/May/17
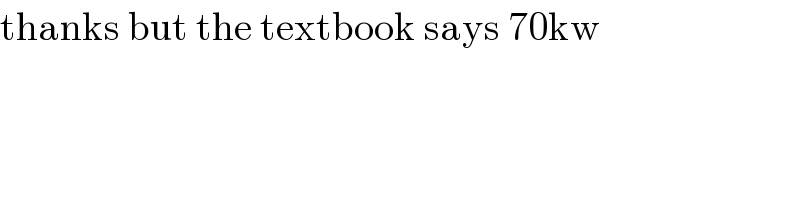
$$\mathrm{thanks}\:\mathrm{but}\:\mathrm{the}\:\mathrm{textbook}\:\mathrm{says}\:\mathrm{70kw} \\ $$
Commented by sandy_suhendra last updated on 22/May/17

$$\mathrm{continued} \\ $$$$\mathrm{P}_{\mathrm{input}\:} =\:\mathrm{100}\:\mathrm{kW} \\ $$$$\mathrm{P}_{\mathrm{output}} \:=\:\eta.\mathrm{P}_{\mathrm{input}} \:=\:\mathrm{0}.\mathrm{7}×\mathrm{100}\:=\:\mathrm{70}\:\mathrm{kW} \\ $$
Commented by chux last updated on 22/May/17

$$\mathrm{thanks}\:\mathrm{boss} \\ $$
