Question Number 47457 by rahul 19 last updated on 10/Nov/18
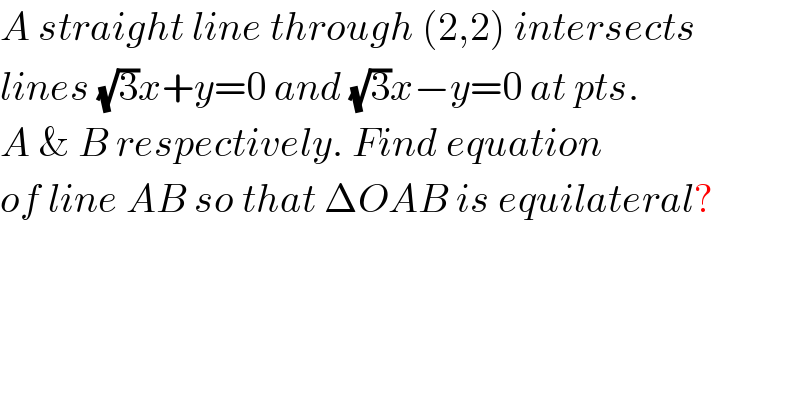
$${A}\:{straight}\:{line}\:{through}\:\left(\mathrm{2},\mathrm{2}\right)\:{intersects} \\ $$$${lines}\:\sqrt{\mathrm{3}}{x}+{y}=\mathrm{0}\:{and}\:\sqrt{\mathrm{3}}{x}−{y}=\mathrm{0}\:{at}\:{pts}. \\ $$$${A}\:\&\:{B}\:{respectively}.\:{Find}\:{equation} \\ $$$${of}\:{line}\:{AB}\:{so}\:{that}\:\Delta{OAB}\:{is}\:{equilateral}? \\ $$
Answered by rahul 19 last updated on 10/Nov/18
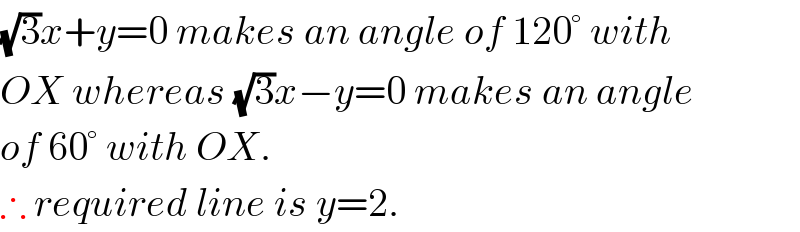
$$\sqrt{\mathrm{3}}{x}+{y}=\mathrm{0}\:{makes}\:{an}\:{angle}\:{of}\:\mathrm{120}°\:{with} \\ $$$${OX}\:{whereas}\:\sqrt{\mathrm{3}}{x}−{y}=\mathrm{0}\:{makes}\:{an}\:{angle} \\ $$$${of}\:\mathrm{60}°\:{with}\:{OX}.\: \\ $$$$\therefore\:{required}\:{line}\:{is}\:{y}=\mathrm{2}. \\ $$
Commented by rahul 19 last updated on 10/Nov/18

$${ok},\:{sir}.. \\ $$
Commented by rahul 19 last updated on 10/Nov/18

$${this}\:{is}\:{hint}\:{given}…. \\ $$$${I}\:{want}\:{to}\:{know}\:{whether}\:{any}\:{other}\: \\ $$$${line}\:{satisfies}\:{the}\:{condition}\:{or}\:{is}\:{it} \\ $$$${unique}\:? \\ $$
Commented by mr W last updated on 10/Nov/18
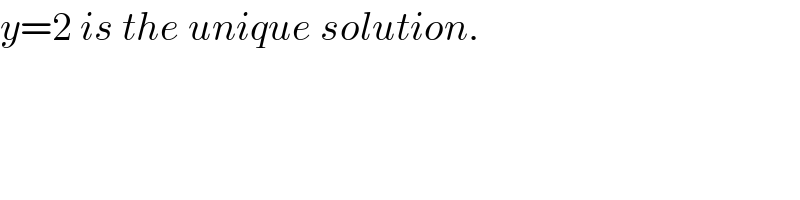
$${y}=\mathrm{2}\:{is}\:{the}\:{unique}\:{solution}. \\ $$
