Question Number 14920 by Tinkutara last updated on 05/Jun/17

$$\mathrm{A}\:\mathrm{swimmer}\:\mathrm{crosses}\:\mathrm{a}\:\mathrm{flowing}\:\mathrm{river}\:\mathrm{of} \\ $$$$\mathrm{width}\:{d}\:\mathrm{to}\:\mathrm{and}\:\mathrm{fro}\:\mathrm{in}\:\mathrm{time}\:{t}_{\mathrm{1}} .\:\mathrm{The}\:\mathrm{time} \\ $$$$\mathrm{taken}\:\mathrm{to}\:\mathrm{cover}\:\mathrm{the}\:\mathrm{same}\:\mathrm{distance}\:\mathrm{up} \\ $$$$\mathrm{and}\:\mathrm{down}\:\mathrm{the}\:\mathrm{stream}\:\mathrm{is}\:{t}_{\mathrm{2}} .\:\mathrm{If}\:{t}_{\mathrm{3}} \:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{time}\:\mathrm{the}\:\mathrm{swimmer}\:\mathrm{would}\:\mathrm{take}\:\mathrm{to}\:\mathrm{swim} \\ $$$$\mathrm{a}\:\mathrm{distance}\:\mathrm{2}{d}\:\mathrm{in}\:\mathrm{still}\:\mathrm{water},\:\mathrm{then}\:\mathrm{prove} \\ $$$$\mathrm{that}\:{t}_{\mathrm{1}} ^{\mathrm{2}} \:=\:{t}_{\mathrm{2}} {t}_{\mathrm{3}} . \\ $$
Answered by ajfour last updated on 05/Jun/17
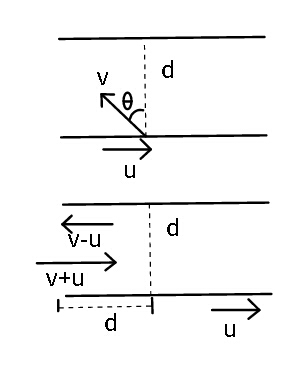
Commented by ajfour last updated on 05/Jun/17
![to go to the other bank and return back to same point (to and fro) swimmer must swim at an angle θ (see fig.) such that vsin 𝛉=u ...(i) t_1 =((2d)/(vcos 𝛉)) ....(ii) to go upstream a distance d and return back time taken is t_2 =(d/(v−u))+(d/(v+u)) ....(iii) to swim a distance 2d in still water time taken is t_3 =((2d)/v) . t_2 t_3 =((2d^2 )/v)(((2v)/(v^2 −u^2 ))) =((4d^2 )/(v^2 −v^2 sin^2 θ)) = (((2d)/(vcos θ)))^2 = t_1 ^2 [see (ii), (iii), and (i) ].](https://www.tinkutara.com/question/Q14925.png)
$${to}\:{go}\:{to}\:{the}\:{other}\:{bank}\:{and}\:{return} \\ $$$${back}\:{to}\:{same}\:{point}\:\left({to}\:{and}\:{fro}\right) \\ $$$${swimmer}\:{must}\:{swim}\:{at}\:{an}\:{angle} \\ $$$$\theta\:\left({see}\:{fig}.\right)\:{such}\:{that} \\ $$$$\:\:\:\boldsymbol{{v}}\mathrm{sin}\:\boldsymbol{\theta}=\boldsymbol{{u}}\:\:\:\:\:…\left({i}\right) \\ $$$$\:\:\boldsymbol{{t}}_{\mathrm{1}} =\frac{\mathrm{2}\boldsymbol{{d}}}{\boldsymbol{{v}}\mathrm{cos}\:\boldsymbol{\theta}}\:\:\:\:\:\:….\left({ii}\right) \\ $$$${to}\:{go}\:{upstream}\:{a}\:{distance}\:\boldsymbol{{d}}\:{and} \\ $$$${return}\:\:{back}\:{time}\:{taken}\:{is} \\ $$$$\:\:\:\boldsymbol{{t}}_{\mathrm{2}} =\frac{\boldsymbol{{d}}}{\boldsymbol{{v}}−\boldsymbol{{u}}}+\frac{\boldsymbol{{d}}}{\boldsymbol{{v}}+\boldsymbol{{u}}}\:\:\:\:….\left({iii}\right) \\ $$$${to}\:{swim}\:{a}\:{distance}\:\mathrm{2}\boldsymbol{{d}}\:{in}\:{still} \\ $$$${water}\:{time}\:{taken}\:{is} \\ $$$$\:\:\boldsymbol{{t}}_{\mathrm{3}} =\frac{\mathrm{2}\boldsymbol{{d}}}{\boldsymbol{{v}}}\:. \\ $$$$\:\:{t}_{\mathrm{2}} {t}_{\mathrm{3}} =\frac{\mathrm{2}{d}^{\mathrm{2}} }{{v}}\left(\frac{\mathrm{2}{v}}{{v}^{\mathrm{2}} −{u}^{\mathrm{2}} }\right)\:=\frac{\mathrm{4}{d}^{\mathrm{2}} }{{v}^{\mathrm{2}} −{v}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$$\:\:\:\:\:\:\:\:=\:\:\left(\frac{\mathrm{2}{d}}{{v}\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \:=\:\boldsymbol{{t}}_{\mathrm{1}} ^{\mathrm{2}} \:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{see}\:\left({ii}\right),\:\left({iii}\right),\:{and}\:\left({i}\right)\:\right]. \\ $$
Commented by Tinkutara last updated on 05/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
