Menu Close

A-teacher-conducts-a-test-for-five-students-He-provides-the-marking-scheme-and-asked-them-to-exchange-their-scripts-such-that-none-of-them-marks-his-own-script-How-many-ways-can-the-students-carry-o

Tinku Tara 0 Comments
Pin




Question Number 111394 by Aina Samuel Temidayo last updated on 03/Sep/20
A teacher conducts a test for five students. He provides the marking scheme and asked them to exchange their scripts such that none of them marks his own script. How many ways can the students carry out the marking?
$$\mathrm{A}\:\mathrm{teacher}\:\mathrm{conducts}\:\mathrm{a}\:\mathrm{test}\:\mathrm{for}\:\mathrm{five} \\ $$$$\mathrm{students}.\:\mathrm{He}\:\mathrm{provides}\:\mathrm{the}\:\mathrm{marking} \\ $$$$\mathrm{scheme}\:\mathrm{and}\:\mathrm{asked}\:\mathrm{them}\:\mathrm{to}\:\mathrm{exchange} \\ $$$$\mathrm{their}\:\mathrm{scripts}\:\mathrm{such}\:\mathrm{that}\:\mathrm{none}\:\mathrm{of}\:\mathrm{them} \\ $$$$\mathrm{marks}\:\mathrm{his}\:\mathrm{own}\:\mathrm{script}.\:\mathrm{How}\:\mathrm{many}\:\mathrm{ways} \\ $$$$\mathrm{can}\:\mathrm{the}\:\mathrm{students}\:\mathrm{carry}\:\mathrm{out}\:\mathrm{the} \\ $$$$\mathrm{marking}? \\ $$
Commented by mr W last updated on 03/Sep/20
44
$$\mathrm{44} \\ $$
Commented by Aina Samuel Temidayo last updated on 03/Sep/20
Solution please?
$$\mathrm{Solution}\:\mathrm{please}? \\ $$
Answered by mr W last updated on 03/Sep/20
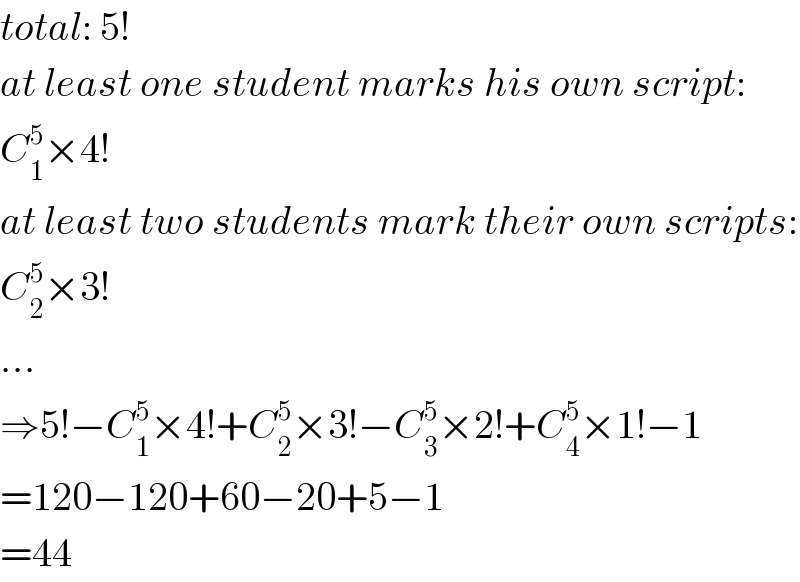
total: 5! at least one student marks his own script: C_1 ^5 ×4! at least two students mark their own scripts: C_2 ^5 ×3! ... ⇒5!−C_1 ^5 ×4!+C_2 ^5 ×3!−C_3 ^5 ×2!+C_4 ^5 ×1!−1 =120−120+60−20+5−1 =44
$${total}:\:\mathrm{5}! \\ $$$${at}\:{least}\:{one}\:{student}\:{marks}\:{his}\:{own}\:{script}: \\ $$$${C}_{\mathrm{1}} ^{\mathrm{5}} ×\mathrm{4}! \\ $$$${at}\:{least}\:{two}\:{students}\:{mark}\:{their}\:{own}\:{scripts}: \\ $$$${C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{3}! \\ $$$$… \\ $$$$\Rightarrow\mathrm{5}!−{C}_{\mathrm{1}} ^{\mathrm{5}} ×\mathrm{4}!+{C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{3}!−{C}_{\mathrm{3}} ^{\mathrm{5}} ×\mathrm{2}!+{C}_{\mathrm{4}} ^{\mathrm{5}} ×\mathrm{1}!−\mathrm{1} \\ $$$$=\mathrm{120}−\mathrm{120}+\mathrm{60}−\mathrm{20}+\mathrm{5}−\mathrm{1} \\ $$$$=\mathrm{44} \\ $$
Commented by Aina Samuel Temidayo last updated on 03/Sep/20
General formula for !n ?
$$\mathrm{General}\:\mathrm{formula}\:\mathrm{for}\:!\mathrm{n}\:? \\ $$
Commented by mr W last updated on 03/Sep/20
or !5=44
$${or} \\ $$$$!\mathrm{5}=\mathrm{44} \\ $$
Commented by mr W last updated on 03/Sep/20
Commented by mr W last updated on 03/Sep/20
as shown above !n=n!Σ_(k=0) ^n (((−1)^k )/(k!)) we have !n=(n−1)[!(n−1)+!(n−2)] !n=[((n!)/e)]
$${as}\:{shown}\:{above} \\ $$$$!{n}={n}!\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!} \\ $$$${we}\:{have} \\ $$$$!{n}=\left({n}−\mathrm{1}\right)\left[!\left({n}−\mathrm{1}\right)+!\left({n}−\mathrm{2}\right)\right] \\ $$$$!{n}=\left[\frac{{n}!}{{e}}\right] \\ $$
Commented by mr W last updated on 03/Sep/20
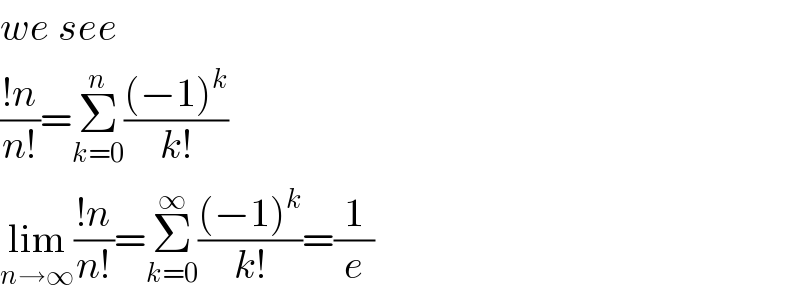
we see ((!n)/(n!))=Σ_(k=0) ^n (((−1)^k )/(k!)) lim_(n→∞) ((!n)/(n!))=Σ_(k=0) ^∞ (((−1)^k )/(k!))=(1/e)
$${we}\:{see} \\ $$$$\frac{!{n}}{{n}!}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{!{n}}{{n}!}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!}=\frac{\mathrm{1}}{{e}} \\ $$
Commented by Aina Samuel Temidayo last updated on 04/Sep/20
Thanks.
$$\mathrm{Thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *