Menu Close

A-train-after-travelling-70-km-from-a-station-A-towards-a-station-B-develops-a-fault-in-the-engine-at-C-and-covers-the-remaining-journey-to-B-at-3-4-of-its-earlier-speed-and-arrives-at-B-1-hour-a

Tinku Tara 0 Comments
Pin




Question Number 17610 by Tinkutara last updated on 08/Jul/17
A train, after travelling 70 km from a station A towards a station B, develops a fault in the engine at C, and covers the remaining journey to B at (3/4) of its earlier speed and arrives at B 1 hour and 20 minutes late. If the fault had developed 35 km further on at D, it would have arrived 20 minutes sooner. Find the speed of the train and the distance from A to B.
$$\mathrm{A}\:\mathrm{train},\:\mathrm{after}\:\mathrm{travelling}\:\mathrm{70}\:\mathrm{km}\:\mathrm{from}\:\mathrm{a} \\ $$$$\mathrm{station}\:\mathrm{A}\:\mathrm{towards}\:\mathrm{a}\:\mathrm{station}\:\mathrm{B},\:\mathrm{develops} \\ $$$$\mathrm{a}\:\mathrm{fault}\:\mathrm{in}\:\mathrm{the}\:\mathrm{engine}\:\mathrm{at}\:\mathrm{C},\:\mathrm{and}\:\mathrm{covers} \\ $$$$\mathrm{the}\:\mathrm{remaining}\:\mathrm{journey}\:\mathrm{to}\:\mathrm{B}\:\mathrm{at}\:\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{of}\:\mathrm{its} \\ $$$$\mathrm{earlier}\:\mathrm{speed}\:\mathrm{and}\:\mathrm{arrives}\:\mathrm{at}\:\mathrm{B}\:\mathrm{1}\:\mathrm{hour} \\ $$$$\mathrm{and}\:\mathrm{20}\:\mathrm{minutes}\:\mathrm{late}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{fault}\:\mathrm{had} \\ $$$$\mathrm{developed}\:\mathrm{35}\:\mathrm{km}\:\mathrm{further}\:\mathrm{on}\:\mathrm{at}\:\mathrm{D},\:\mathrm{it} \\ $$$$\mathrm{would}\:\mathrm{have}\:\mathrm{arrived}\:\mathrm{20}\:\mathrm{minutes}\:\mathrm{sooner}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{the}\:\mathrm{train}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{distance}\:\mathrm{from}\:\mathrm{A}\:\mathrm{to}\:\mathrm{B}. \\ $$
Commented by Tinkutara last updated on 08/Jul/17
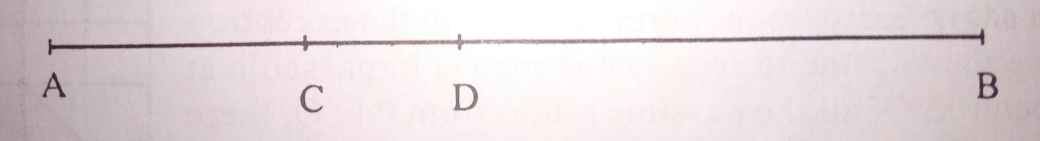
Answered by alex041103 last updated on 08/Jul/17
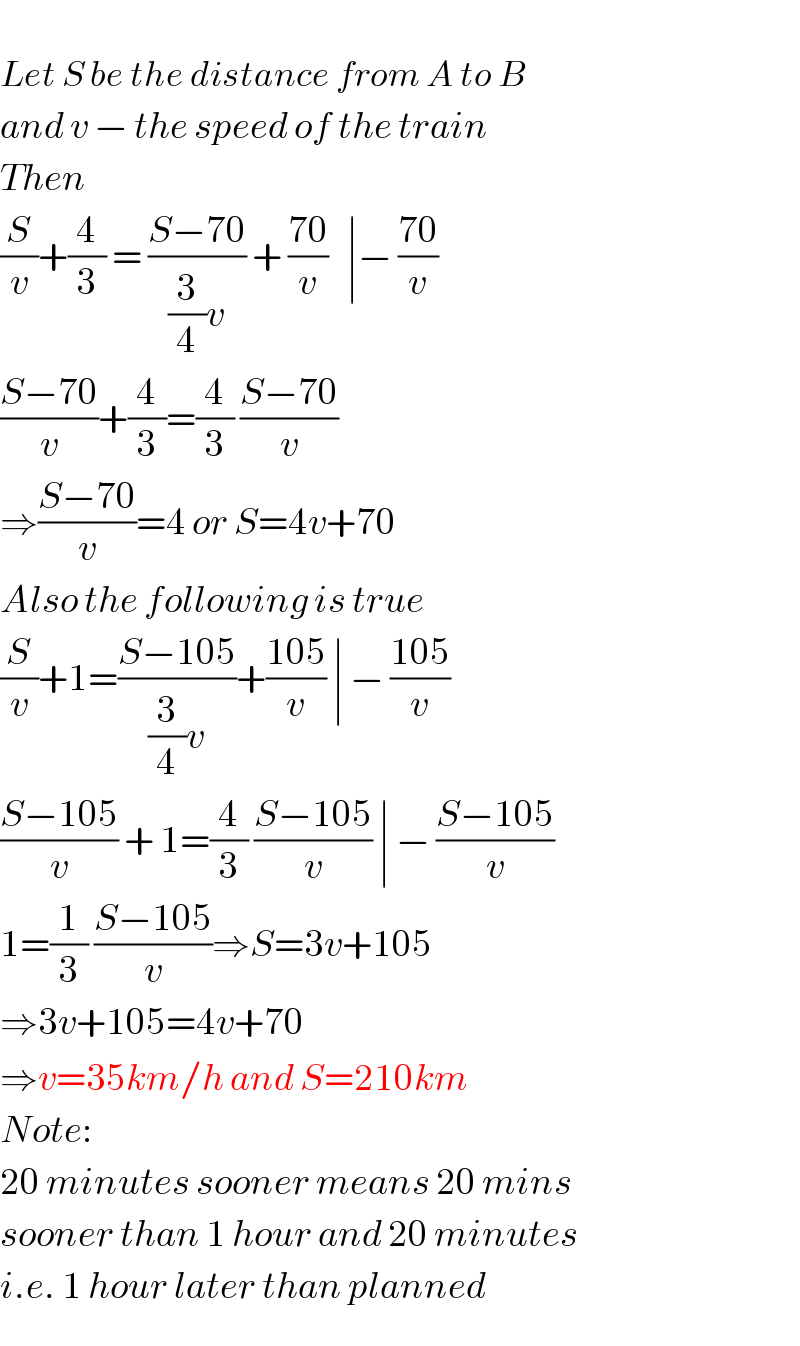
Let S be the distance from A to B and v − the speed of the train Then (S/v)+(4/3) = ((S−70)/((3/4)v)) + ((70)/v) ∣− ((70)/v) ((S−70)/v)+(4/3)=(4/3) ((S−70)/v) ⇒((S−70)/v)=4 or S=4v+70 Also the following is true (S/v)+1=((S−105)/((3/4)v))+((105)/v) ∣ − ((105)/v) ((S−105)/v) + 1=(4/3) ((S−105)/v) ∣ − ((S−105)/v) 1=(1/3) ((S−105)/v)⇒S=3v+105 ⇒3v+105=4v+70 ⇒v=35km/h and S=210km Note: 20 minutes sooner means 20 mins sooner than 1 hour and 20 minutes i.e. 1 hour later than planned
$$ \\ $$$${Let}\:{S}\:{be}\:{the}\:{distance}\:{from}\:{A}\:{to}\:{B} \\ $$$${and}\:{v}\:−\:{the}\:{speed}\:{of}\:{the}\:{train} \\ $$$${Then} \\ $$$$\frac{{S}}{{v}}+\frac{\mathrm{4}}{\mathrm{3}}\:=\:\frac{{S}−\mathrm{70}}{\frac{\mathrm{3}}{\mathrm{4}}{v}}\:+\:\frac{\mathrm{70}}{{v}}\:\:\:\mid−\:\frac{\mathrm{70}}{{v}} \\ $$$$\frac{{S}−\mathrm{70}}{{v}}+\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{3}}\:\frac{{S}−\mathrm{70}}{{v}} \\ $$$$\Rightarrow\frac{{S}−\mathrm{70}}{{v}}=\mathrm{4}\:{or}\:{S}=\mathrm{4}{v}+\mathrm{70} \\ $$$${Also}\:{the}\:{following}\:{is}\:{true} \\ $$$$\frac{{S}}{{v}}+\mathrm{1}=\frac{{S}−\mathrm{105}}{\frac{\mathrm{3}}{\mathrm{4}}{v}}+\frac{\mathrm{105}}{{v}}\:\mid\:−\:\frac{\mathrm{105}}{{v}} \\ $$$$\frac{{S}−\mathrm{105}}{{v}}\:+\:\mathrm{1}=\frac{\mathrm{4}}{\mathrm{3}}\:\frac{{S}−\mathrm{105}}{{v}}\:\mid\:−\:\frac{{S}−\mathrm{105}}{{v}} \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{S}−\mathrm{105}}{{v}}\Rightarrow{S}=\mathrm{3}{v}+\mathrm{105} \\ $$$$\Rightarrow\mathrm{3}{v}+\mathrm{105}=\mathrm{4}{v}+\mathrm{70} \\ $$$$\Rightarrow{v}=\mathrm{35}{km}/{h}\:{and}\:{S}=\mathrm{210}{km} \\ $$$${Note}: \\ $$$$\mathrm{20}\:{minutes}\:{sooner}\:{means}\:\mathrm{20}\:{mins} \\ $$$${sooner}\:{than}\:\mathrm{1}\:{hour}\:{and}\:\mathrm{20}\:{minutes} \\ $$$${i}.{e}.\:\mathrm{1}\:{hour}\:{later}\:{than}\:{planned} \\ $$
Commented by Tinkutara last updated on 09/Jul/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *