Question Number 110782 by Aina Samuel Temidayo last updated on 30/Aug/20

$$\mathrm{A}\:\mathrm{triangle}\:\mathrm{has}\:\mathrm{area}\:\mathrm{15}\:\mathrm{and} \\ $$$$\mathrm{circumradius}\:\mathrm{12}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of} \\ $$$$\mathrm{its}\:\mathrm{heights}. \\ $$
Answered by som(math1967) last updated on 30/Aug/20
![(1/2)bcsinA=15 bc×(a/(24))=30 [∵sinA=(a/(2R))] abc=30×24 let heights are h_1 ,h_2 ,h_3 ∴(1/2)×h_1 ×a=(1/2)×bc×sinA (1/2)×h_2 ×b=(1/2)×casinB (1/2)×h_3 ×c=(1/2)×absinC ∴h_1 ×h_2 ×h_3 =abcsinAsinBsinC =abc×(a/(24))×(b/(24))×(c/(24)) =((a^2 b^2 c^2 )/(24×24×24)) =((30×30×24×24)/(24×24×24)) =((900)/(24))=((75)/2)](https://www.tinkutara.com/question/Q110793.png)
$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{bcsinA}=\mathrm{15} \\ $$$$\mathrm{bc}×\frac{\mathrm{a}}{\mathrm{24}}=\mathrm{30}\:\left[\because\mathrm{sinA}=\frac{\mathrm{a}}{\mathrm{2R}}\right] \\ $$$$\mathrm{abc}=\mathrm{30}×\mathrm{24} \\ $$$$\mathrm{let}\:\mathrm{heights}\:\mathrm{are}\:\mathrm{h}_{\mathrm{1}} ,\mathrm{h}_{\mathrm{2}} ,\mathrm{h}_{\mathrm{3}} \\ $$$$\therefore\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{h}_{\mathrm{1}} ×\mathrm{a}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{bc}×\mathrm{sinA} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{h}_{\mathrm{2}} ×\mathrm{b}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{casinB} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{h}_{\mathrm{3}} ×\mathrm{c}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{absinC} \\ $$$$\therefore\mathrm{h}_{\mathrm{1}} ×\mathrm{h}_{\mathrm{2}} ×\mathrm{h}_{\mathrm{3}} =\mathrm{abcsinAsinBsinC} \\ $$$$=\mathrm{abc}×\frac{\mathrm{a}}{\mathrm{24}}×\frac{\mathrm{b}}{\mathrm{24}}×\frac{\mathrm{c}}{\mathrm{24}} \\ $$$$=\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\mathrm{24}×\mathrm{24}×\mathrm{24}} \\ $$$$=\frac{\mathrm{30}×\mathrm{30}×\mathrm{24}×\mathrm{24}}{\mathrm{24}×\mathrm{24}×\mathrm{24}} \\ $$$$=\frac{\mathrm{900}}{\mathrm{24}}=\frac{\mathrm{75}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 30/Aug/20
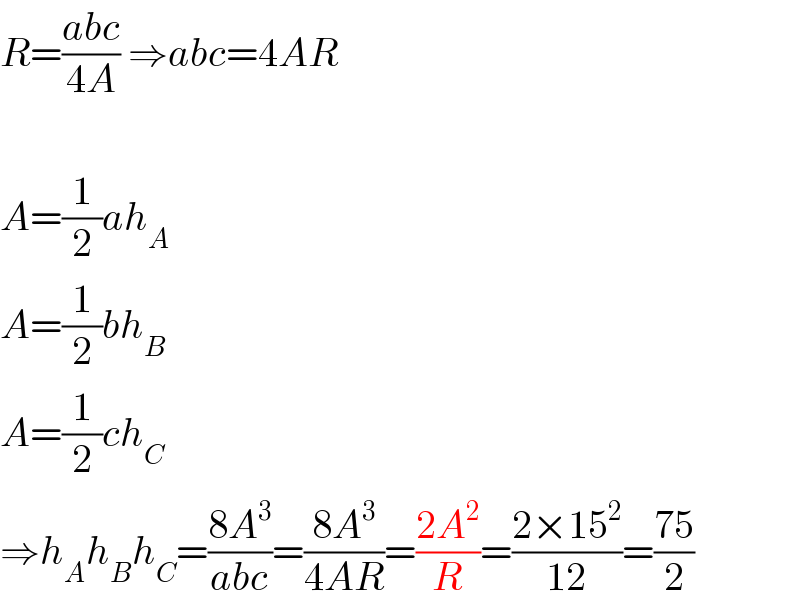
$${R}=\frac{{abc}}{\mathrm{4}{A}}\:\Rightarrow{abc}=\mathrm{4}{AR} \\ $$$$ \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}{ah}_{{A}} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}{bh}_{{B}} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}{ch}_{{C}} \\ $$$$\Rightarrow{h}_{{A}} {h}_{{B}} {h}_{{C}} =\frac{\mathrm{8}{A}^{\mathrm{3}} }{{abc}}=\frac{\mathrm{8}{A}^{\mathrm{3}} }{\mathrm{4}{AR}}=\frac{\mathrm{2}{A}^{\mathrm{2}} }{{R}}=\frac{\mathrm{2}×\mathrm{15}^{\mathrm{2}} }{\mathrm{12}}=\frac{\mathrm{75}}{\mathrm{2}} \\ $$
Commented by Aina Samuel Temidayo last updated on 30/Aug/20

$$\mathrm{Thanks}. \\ $$
