Question Number 182108 by Tawa11 last updated on 04/Dec/22

A truck, P traveling at 54km/hr passes through a point at 10:30am, while
another truck, Q traveling at 90km/hr passes through this
same point 30 minutes later. At what time will truck Q overtake P?
another truck, Q traveling at 90km/hr passes through this
same point 30 minutes later. At what time will truck Q overtake P?
Answered by Acem last updated on 04/Dec/22

$$\:\frac{{v}_{\mathrm{2}} }{{v}_{\mathrm{1}} }=\:\frac{{x}+\mathrm{27}}{{x}}\:\:\:;\:\mathrm{27}\:=\:{the}\:{distance}\:{traveled}\:{by}\:{P}\:{in}\:\mathrm{30}\:{min} \\ $$$$\:{x}:\:{the}\:{distance}\:{traveled}\:{by}\:{P}\:{at}\:{the}\:{moment}\:{the}\:{other}\:{reaches}\:{it} \\ $$$$\:{x}=\:\mathrm{40}.\mathrm{5}\:{km}\:\Rightarrow\:{Time}=\:\frac{{x}}{{v}_{\mathrm{1}} }=\:\mathrm{45}\:{min} \\ $$$$\:{The}\:{speed}\:{diff}.=\:\mathrm{10}\:{m}.{s}^{−\mathrm{1}} \\ $$$$\:{If}\:{length}\:{of}\:{P}\:{is}\:\mathrm{10}{m}\::\:{Q}\:{needs}\:\mathrm{1}{s}\:{to}\:{overtake}\:{it} \\ $$$$\:{Real}\:{time}=\:\mathrm{45}\:{min}\:{and}\:{one}\:{second} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 04/Dec/22
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sirs} \\ $$
Commented by Acem last updated on 04/Dec/22

$${You}'{re}\:{very}\:{welcome},\:{but}\:{don}'{t}\:{forget}\:{the} \\ $$$$\:\mathrm{1}\:{sec}\:\&\:{moving}\:{eyebrows}\:{up}\:{down}\:{to}\:{the} \\ $$$$\left.\:{P}\:'{s}\:{driver}\:{during}\:{the}\:{overtake}\::\right) \\ $$
Answered by mr W last updated on 04/Dec/22
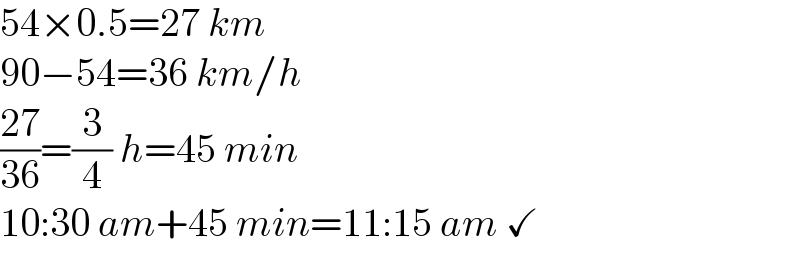
$$\mathrm{54}×\mathrm{0}.\mathrm{5}=\mathrm{27}\:{km} \\ $$$$\mathrm{90}−\mathrm{54}=\mathrm{36}\:{km}/{h} \\ $$$$\frac{\mathrm{27}}{\mathrm{36}}=\frac{\mathrm{3}}{\mathrm{4}}\:{h}=\mathrm{45}\:{min} \\ $$$$\mathrm{10}:\mathrm{30}\:{am}+\mathrm{45}\:{min}=\mathrm{11}:\mathrm{15}\:{am}\:\checkmark \\ $$
Commented by Tawa11 last updated on 04/Dec/22
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sirs} \\ $$
Commented by sciencestudent last updated on 09/Dec/22
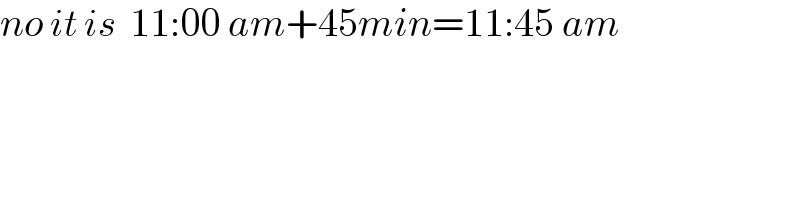
$${no}\:{it}\:{is}\:\:\mathrm{11}:\mathrm{00}\:{am}+\mathrm{45}{min}=\mathrm{11}:\mathrm{45}\:{am} \\ $$
