Question Number 18092 by Tinkutara last updated on 15/Jul/17
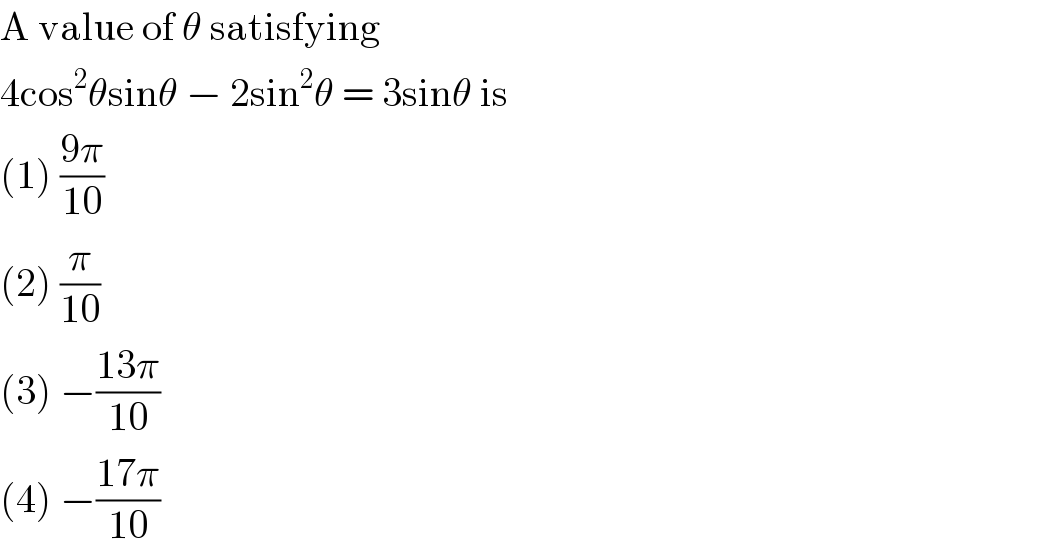
$$\mathrm{A}\:\mathrm{value}\:\mathrm{of}\:\theta\:\mathrm{satisfying} \\ $$$$\mathrm{4cos}^{\mathrm{2}} \theta\mathrm{sin}\theta\:−\:\mathrm{2sin}^{\mathrm{2}} \theta\:=\:\mathrm{3sin}\theta\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\frac{\mathrm{9}\pi}{\mathrm{10}} \\ $$$$\left(\mathrm{2}\right)\:\frac{\pi}{\mathrm{10}} \\ $$$$\left(\mathrm{3}\right)\:−\frac{\mathrm{13}\pi}{\mathrm{10}} \\ $$$$\left(\mathrm{4}\right)\:−\frac{\mathrm{17}\pi}{\mathrm{10}} \\ $$
Answered by ajfour last updated on 15/Jul/17

$$\left(\mathrm{sin}\:\theta\right)\left(\mathrm{4cos}\:^{\mathrm{2}} \theta−\mathrm{2sin}\:\theta−\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta=\mathrm{0}\:\:,\:\mathrm{or} \\ $$$$\:\:\:\:\:\:\mathrm{4}−\mathrm{4sin}\:^{\mathrm{2}} \theta−\mathrm{2sin}\:\theta−\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{sin}\:^{\mathrm{2}} \theta+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\Rightarrow\:\:\:\:\:\:\:\left(\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{16}}=\frac{\mathrm{5}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\mathrm{sin}\:\theta=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\theta=\frac{\pi}{\mathrm{10}},\:−\frac{\mathrm{3}\pi}{\mathrm{10}},\:\mathrm{and}\:\mathrm{so}\:\mathrm{on}.. \\ $$$$\mathrm{Among}\:\mathrm{the}\:\mathrm{options},\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{with} \\ $$$$\:\:\theta=\frac{\pi}{\mathrm{10}}\:,\:\frac{\mathrm{9}\pi}{\mathrm{10}}\:\:\mathrm{are}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{options}. \\ $$
Commented by Tinkutara last updated on 15/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
