Question Number 38924 by NECx last updated on 01/Jul/18

$${A}\:{wave}\:{has}\:{a}\:{wavelength}\:{of}\:\mathrm{1}.\mathrm{5}{m}, \\ $$$${calculate}\:{the}\:{phase}\:{angle}\:{between} \\ $$$${a}\:{point}\:\mathrm{0}.\mathrm{25}{m}\:{from}\:{the}\:{peak}\:{of}\:{the} \\ $$$${wave}\:{and}\:{another}\:{point}\:\mathrm{1}{m}\:{further} \\ $$$${along}\:{the}\:{same}\:{peak}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jul/18
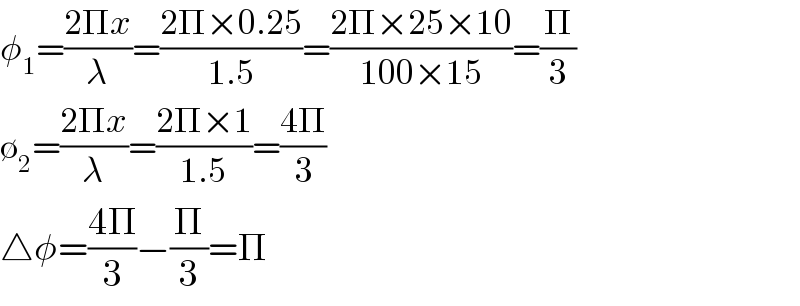
$$\phi_{\mathrm{1}} =\frac{\mathrm{2}\Pi{x}}{\lambda}=\frac{\mathrm{2}\Pi×\mathrm{0}.\mathrm{25}}{\mathrm{1}.\mathrm{5}}=\frac{\mathrm{2}\Pi×\mathrm{25}×\mathrm{10}}{\mathrm{100}×\mathrm{15}}=\frac{\Pi}{\mathrm{3}} \\ $$$$\emptyset_{\mathrm{2}} =\frac{\mathrm{2}\Pi{x}}{\lambda}=\frac{\mathrm{2}\Pi×\mathrm{1}}{\mathrm{1}.\mathrm{5}}=\frac{\mathrm{4}\Pi}{\mathrm{3}} \\ $$$$\bigtriangleup\phi=\frac{\mathrm{4}\Pi}{\mathrm{3}}−\frac{\Pi}{\mathrm{3}}=\Pi \\ $$
