Question Number 55344 by Necxx last updated on 21/Feb/19

$${A}\:{whatsapp}\:{group}\:{contains}\:\mathrm{7}\:{women} \\ $$$${and}\:\mathrm{3}\:{men}.{If}\:{they}\:{are}\:{leaving} \\ $$$${the}\:{group}\:{one}\:{at}\:{a}\:{time}\:{from}\:{the} \\ $$$${group}\:{what}\:{is}\:{the}\:{probability}\:{of}\:{a} \\ $$$${woman}\:{leaving}\:{then}\:{a}\:{man}\:{leaving} \\ $$$${and}\:{so}\:{on}\:{alternately}\:{until}\:{only}\:{a} \\ $$$${woman}\:{is}\:{remaining}? \\ $$$$ \\ $$
Commented by mr W last updated on 22/Feb/19
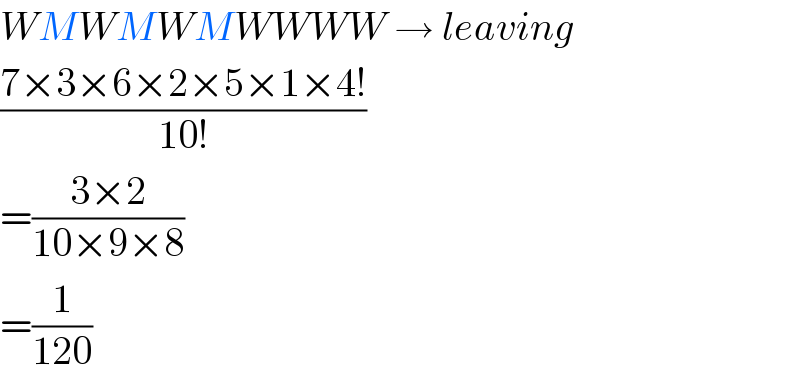
$${WMWMWMWWWW}\:\rightarrow\:{leaving} \\ $$$$\frac{\mathrm{7}×\mathrm{3}×\mathrm{6}×\mathrm{2}×\mathrm{5}×\mathrm{1}×\mathrm{4}!}{\mathrm{10}!} \\ $$$$=\frac{\mathrm{3}×\mathrm{2}}{\mathrm{10}×\mathrm{9}×\mathrm{8}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{120}} \\ $$
Commented by necx1 last updated on 23/Feb/19

$${yeah}….\:{Thanks} \\ $$
Commented by rahul 19 last updated on 23/Feb/19
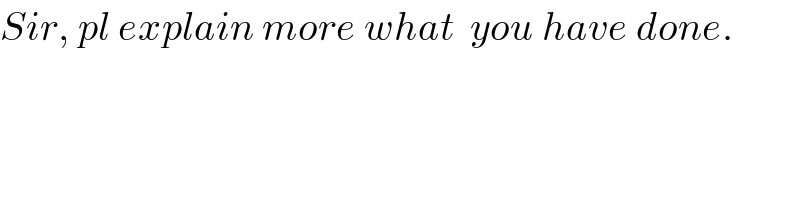
$${Sir},\:{pl}\:{explain}\:{more}\:{what}\:\:{you}\:{have}\:{done}. \\ $$
Commented by mr W last updated on 24/Feb/19

$${total}\:{number}\:{of}\:{ways}\:{to}\:{arrange}\:\mathrm{10} \\ $$$${persons}\:{is}\:\mathrm{10}!. \\ $$$${such}\:{that}\:{the}\:{persons}\:{leave}\:{whatsapp} \\ $$$${in}\:{the}\:{way}\:{as}\:{requested}\:{in}\:{the}\:{question}, \\ $$$${the}\:{persons}\:{should}\:{be}\:{arranged}\:{like} \\ $$$${this}: \\ $$$${WMWMWMWWWW}\rightarrow{leaving}\:{whatsapp} \\ $$$${with}\:{W}={woman},\:{M}={man} \\ $$$${there}\:{are}\:\mathrm{7}!\mathrm{3}!\:{such}\:{arrangements}, \\ $$$${therefore}\:{the}\:{probability}\:{is} \\ $$$$\frac{\mathrm{7}!\mathrm{3}!}{\mathrm{10}!}=\frac{\mathrm{3}!}{\mathrm{10}×\mathrm{9}×\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{120}} \\ $$
Commented by rahul 19 last updated on 25/Feb/19

$${thank}\:{U}\:{sir}! \\ $$
Commented by rahul 19 last updated on 25/Feb/19
Today is 25th Feb'19 ...
why my comment shows 24th Feb'19 ?
some technical error ...
