Menu Close

A-wire-of-mass-9-8-10-3-kg-per-meter-passes-over-a-frictionless-pulley-fixed-on-the-top-of-an-inclined-frictionless-plane-which-makes-an-angle-of-30-with-the-horizontal-Masses-M-1-and-M-2-ar

Tinku Tara 0 Comments
Pin




Question Number 21870 by Tinkutara last updated on 05/Oct/17
A wire of mass 9.8 × 10^(−3) kg per meter passes over a frictionless pulley fixed on the top of an inclined frictionless plane which makes an angle of 30° with the horizontal. Masses M_1 and M_2 are tied at the two ends of the wire. The mass M_1 rests on the plane and the mass M_2 hangs freely vertically downward. The whole system is in equilibrium. Now a transverse wave propagates along the wire with a velocity of 100 m/s. Find M_1 and M_2 (g = 9.8 m/s^2 ).
$$\mathrm{A}\:\mathrm{wire}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{9}.\mathrm{8}\:×\:\mathrm{10}^{−\mathrm{3}} \:\mathrm{kg}\:\mathrm{per}\:\mathrm{meter} \\ $$$$\mathrm{passes}\:\mathrm{over}\:\mathrm{a}\:\mathrm{frictionless}\:\mathrm{pulley}\:\mathrm{fixed} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{top}\:\mathrm{of}\:\mathrm{an}\:\mathrm{inclined}\:\mathrm{frictionless} \\ $$$$\mathrm{plane}\:\mathrm{which}\:\mathrm{makes}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{30}°\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{horizontal}.\:\mathrm{Masses}\:{M}_{\mathrm{1}} \:\mathrm{and}\:{M}_{\mathrm{2}} \:\mathrm{are} \\ $$$$\mathrm{tied}\:\mathrm{at}\:\mathrm{the}\:\mathrm{two}\:\mathrm{ends}\:\mathrm{of}\:\mathrm{the}\:\mathrm{wire}.\:\mathrm{The} \\ $$$$\mathrm{mass}\:{M}_{\mathrm{1}} \:\mathrm{rests}\:\mathrm{on}\:\mathrm{the}\:\mathrm{plane}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{mass}\:{M}_{\mathrm{2}} \:\mathrm{hangs}\:\mathrm{freely}\:\mathrm{vertically} \\ $$$$\mathrm{downward}.\:\mathrm{The}\:\mathrm{whole}\:\mathrm{system}\:\mathrm{is}\:\mathrm{in} \\ $$$$\mathrm{equilibrium}.\:\mathrm{Now}\:\mathrm{a}\:\mathrm{transverse}\:\mathrm{wave} \\ $$$$\mathrm{propagates}\:\mathrm{along}\:\mathrm{the}\:\mathrm{wire}\:\mathrm{with}\:\mathrm{a} \\ $$$$\mathrm{velocity}\:\mathrm{of}\:\mathrm{100}\:\mathrm{m}/\mathrm{s}.\:\mathrm{Find}\:{M}_{\mathrm{1}} \:\mathrm{and}\:{M}_{\mathrm{2}} \\ $$$$\left({g}\:=\:\mathrm{9}.\mathrm{8}\:\mathrm{m}/\mathrm{s}^{\mathrm{2}} \right). \\ $$
Answered by ajfour last updated on 05/Oct/17
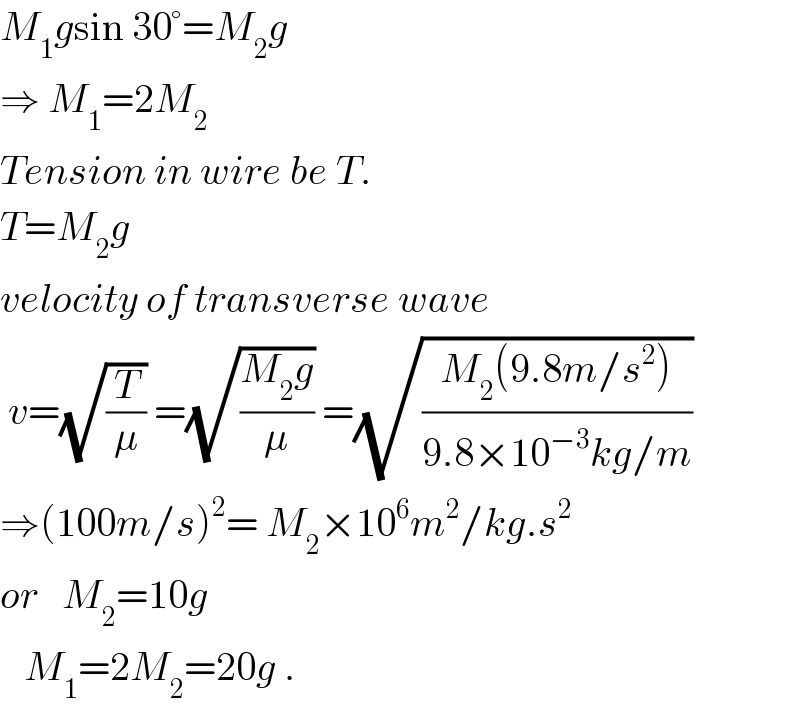
M_1 gsin 30°=M_2 g ⇒ M_1 =2M_2 Tension in wire be T. T=M_2 g velocity of transverse wave v=(√(T/μ)) =(√((M_2 g)/μ)) =(√((M_2 (9.8m/s^2 ))/(9.8×10^(−3) kg/m))) ⇒(100m/s)^2 = M_2 ×10^6 m^2 /kg.s^2 or M_2 =10g M_1 =2M_2 =20g .
$${M}_{\mathrm{1}} {g}\mathrm{sin}\:\mathrm{30}°={M}_{\mathrm{2}} {g} \\ $$$$\Rightarrow\:{M}_{\mathrm{1}} =\mathrm{2}{M}_{\mathrm{2}} \\ $$$${Tension}\:{in}\:{wire}\:{be}\:{T}. \\ $$$${T}={M}_{\mathrm{2}} {g} \\ $$$${velocity}\:{of}\:{transverse}\:{wave}\: \\ $$$$\:{v}=\sqrt{\frac{{T}}{\mu}}\:=\sqrt{\frac{{M}_{\mathrm{2}} {g}}{\mu}}\:=\sqrt{\frac{{M}_{\mathrm{2}} \left(\mathrm{9}.\mathrm{8}{m}/{s}^{\mathrm{2}} \right)}{\mathrm{9}.\mathrm{8}×\mathrm{10}^{−\mathrm{3}} {kg}/{m}}}\: \\ $$$$\Rightarrow\left(\mathrm{100}{m}/{s}\right)^{\mathrm{2}} =\:{M}_{\mathrm{2}} ×\mathrm{10}^{\mathrm{6}} {m}^{\mathrm{2}} /{kg}.{s}^{\mathrm{2}} \\ $$$${or}\:\:\:{M}_{\mathrm{2}} =\mathrm{10}{g} \\ $$$$\:\:\:{M}_{\mathrm{1}} =\mathrm{2}{M}_{\mathrm{2}} =\mathrm{20}{g}\:. \\ $$
Commented by Tinkutara last updated on 06/Oct/17
Thank you very much Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *