Menu Close

A-wooden-block-of-mass-10-gm-is-dropped-from-the-top-of-a-tower-100-m-high-Simultaneously-a-bullet-of-mass-10-gm-is-fired-from-the-foot-of-the-tower-vertically-upwards-with-a-velocity-of-100-m-sec-

Tinku Tara 0 Comments
Pin




Question Number 23520 by Tinkutara last updated on 01/Nov/17
A wooden block of mass 10 gm is dropped from the top of a tower 100 m high. Simultaneously, a bullet of mass 10 gm is fired from the foot of the tower vertically upwards with a velocity of 100 m/sec. If the bullet is embedded in it, how high will it rise above the tower before it starts falling? (Consider g = 10 m/sec^2 )
$$\mathrm{A}\:\mathrm{wooden}\:\mathrm{block}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{10}\:\mathrm{gm}\:\mathrm{is} \\ $$$$\mathrm{dropped}\:\mathrm{from}\:\mathrm{the}\:\mathrm{top}\:\mathrm{of}\:\mathrm{a}\:\mathrm{tower}\:\mathrm{100}\:\mathrm{m} \\ $$$$\mathrm{high}.\:\mathrm{Simultaneously},\:\mathrm{a}\:\mathrm{bullet}\:\mathrm{of}\:\mathrm{mass} \\ $$$$\mathrm{10}\:\mathrm{gm}\:\mathrm{is}\:\mathrm{fired}\:\mathrm{from}\:\mathrm{the}\:\mathrm{foot}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tower} \\ $$$$\mathrm{vertically}\:\mathrm{upwards}\:\mathrm{with}\:\mathrm{a}\:\mathrm{velocity}\:\mathrm{of} \\ $$$$\mathrm{100}\:\mathrm{m}/\mathrm{sec}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{bullet}\:\mathrm{is}\:\mathrm{embedded}\:\mathrm{in} \\ $$$$\mathrm{it},\:\mathrm{how}\:\mathrm{high}\:\mathrm{will}\:\mathrm{it}\:\mathrm{rise}\:\mathrm{above}\:\mathrm{the}\:\mathrm{tower} \\ $$$$\mathrm{before}\:\mathrm{it}\:\mathrm{starts}\:\mathrm{falling}?\:\left(\mathrm{Consider}\:{g}\:=\right. \\ $$$$\left.\mathrm{10}\:\mathrm{m}/\mathrm{sec}^{\mathrm{2}} \right) \\ $$
Commented by Tinkutara last updated on 01/Nov/17
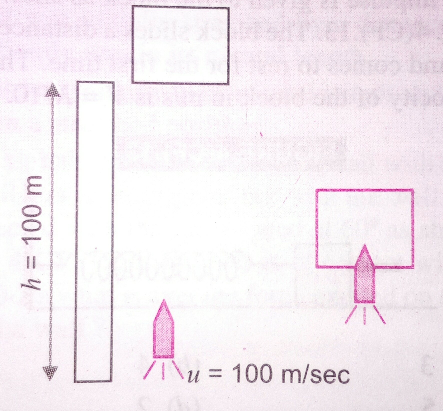
Commented by mrW1 last updated on 01/Nov/17
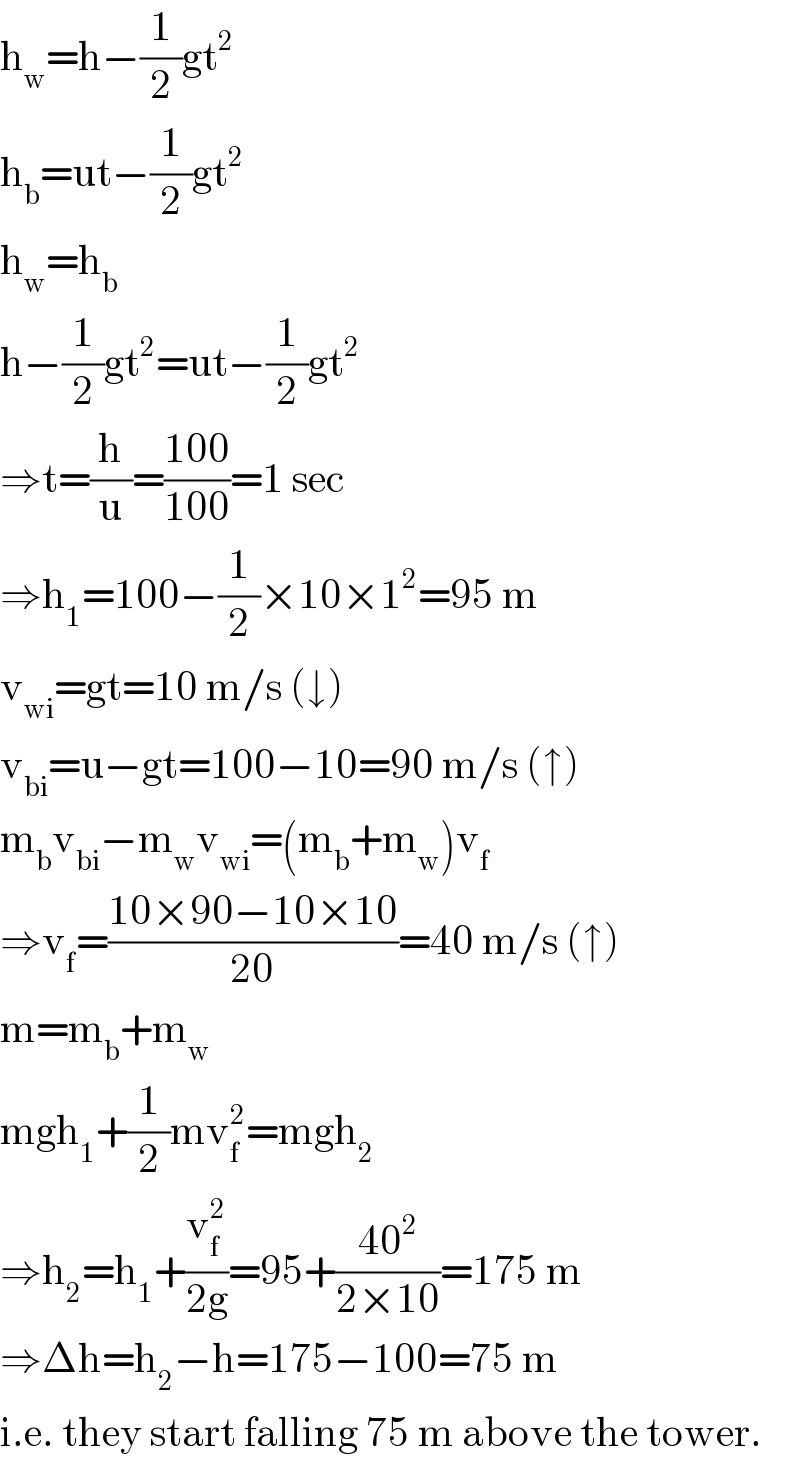
h_w =h−(1/2)gt^2 h_b =ut−(1/2)gt^2 h_w =h_b h−(1/2)gt^2 =ut−(1/2)gt^2 ⇒t=(h/u)=((100)/(100))=1 sec ⇒h_1 =100−(1/2)×10×1^2 =95 m v_(wi) =gt=10 m/s (↓) v_(bi) =u−gt=100−10=90 m/s (↑) m_b v_(bi) −m_w v_(wi) =(m_b +m_w )v_f ⇒v_f =((10×90−10×10)/(20))=40 m/s (↑) m=m_b +m_w mgh_1 +(1/2)mv_f ^2 =mgh_2 ⇒h_2 =h_1 +(v_f ^2 /(2g))=95+((40^2 )/(2×10))=175 m ⇒Δh=h_2 −h=175−100=75 m i.e. they start falling 75 m above the tower.
$$\mathrm{h}_{\mathrm{w}} =\mathrm{h}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} \\ $$$$\mathrm{h}_{\mathrm{b}} =\mathrm{ut}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} \\ $$$$\mathrm{h}_{\mathrm{w}} =\mathrm{h}_{\mathrm{b}} \\ $$$$\mathrm{h}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} =\mathrm{ut}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{t}=\frac{\mathrm{h}}{\mathrm{u}}=\frac{\mathrm{100}}{\mathrm{100}}=\mathrm{1}\:\mathrm{sec} \\ $$$$\Rightarrow\mathrm{h}_{\mathrm{1}} =\mathrm{100}−\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{10}×\mathrm{1}^{\mathrm{2}} =\mathrm{95}\:\mathrm{m} \\ $$$$\mathrm{v}_{\mathrm{wi}} =\mathrm{gt}=\mathrm{10}\:\mathrm{m}/\mathrm{s}\:\left(\downarrow\right) \\ $$$$\mathrm{v}_{\mathrm{bi}} =\mathrm{u}−\mathrm{gt}=\mathrm{100}−\mathrm{10}=\mathrm{90}\:\mathrm{m}/\mathrm{s}\:\left(\uparrow\right) \\ $$$$\mathrm{m}_{\mathrm{b}} \mathrm{v}_{\mathrm{bi}} −\mathrm{m}_{\mathrm{w}} \mathrm{v}_{\mathrm{wi}} =\left(\mathrm{m}_{\mathrm{b}} +\mathrm{m}_{\mathrm{w}} \right)\mathrm{v}_{\mathrm{f}} \\ $$$$\Rightarrow\mathrm{v}_{\mathrm{f}} =\frac{\mathrm{10}×\mathrm{90}−\mathrm{10}×\mathrm{10}}{\mathrm{20}}=\mathrm{40}\:\mathrm{m}/\mathrm{s}\:\left(\uparrow\right) \\ $$$$\mathrm{m}=\mathrm{m}_{\mathrm{b}} +\mathrm{m}_{\mathrm{w}} \\ $$$$\mathrm{mgh}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{mv}_{\mathrm{f}} ^{\mathrm{2}} =\mathrm{mgh}_{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{h}_{\mathrm{2}} =\mathrm{h}_{\mathrm{1}} +\frac{\mathrm{v}_{\mathrm{f}} ^{\mathrm{2}} }{\mathrm{2g}}=\mathrm{95}+\frac{\mathrm{40}^{\mathrm{2}} }{\mathrm{2}×\mathrm{10}}=\mathrm{175}\:\mathrm{m} \\ $$$$\Rightarrow\Delta\mathrm{h}=\mathrm{h}_{\mathrm{2}} −\mathrm{h}=\mathrm{175}−\mathrm{100}=\mathrm{75}\:\mathrm{m} \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{they}\:\mathrm{start}\:\mathrm{falling}\:\mathrm{75}\:\mathrm{m}\:\mathrm{above}\:\mathrm{the}\:\mathrm{tower}. \\ $$
Commented by Tinkutara last updated on 01/Nov/17
Thank you very much Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *