a-x-1-ax-dx-a-gt-0-

Question Number 127190 by bramlexs22 last updated on 27/Dec/20

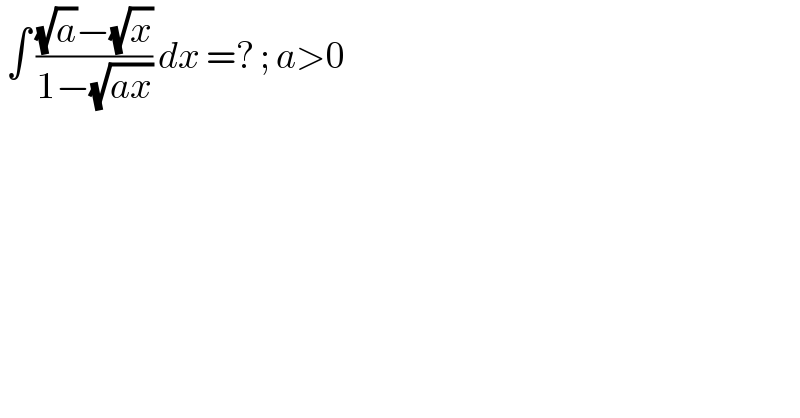
$$\:\int\:\frac{\sqrt{{a}}−\sqrt{{x}}}{\mathrm{1}−\sqrt{{ax}}}\:{dx}\:=?\:;\:{a}>\mathrm{0} \\ $$

Answered by Dwaipayan Shikari last updated on 27/Dec/20

⇒ax=u^2 ⇒a=2u(du/dx) 2∫(((√a)−(u/( (√a))))/(1−u)).(u/a)du = (2/( (√a^3 )))∫((a−u)/(1−u))du=(2/( (√a^3 )))u+(2/( (√a^3 )))∫((a−1)/(1−u))du =(2/( (√a^3 )))u−((2(a−1))/( (√a^3 )))log(1−u)+C=((2(√x))/a)−((2(a−1))/( (√a^3 )))log(1−(√(ax)))+C

$$\Rightarrow{ax}={u}^{\mathrm{2}} \Rightarrow{a}=\mathrm{2}{u}\frac{{du}}{{dx}} \\ $$$$\mathrm{2}\int\frac{\sqrt{{a}}−\frac{{u}}{\:\sqrt{{a}}}}{\mathrm{1}−{u}}.\frac{{u}}{{a}}{du}\:=\:\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{3}} }}\int\frac{{a}−{u}}{\mathrm{1}−{u}}{du}=\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{3}} }}{u}+\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{3}} }}\int\frac{{a}−\mathrm{1}}{\mathrm{1}−{u}}{du} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{3}} }}{u}−\frac{\mathrm{2}\left({a}−\mathrm{1}\right)}{\:\sqrt{{a}^{\mathrm{3}} }}{log}\left(\mathrm{1}−{u}\right)+{C}=\frac{\mathrm{2}\sqrt{{x}}}{{a}}−\frac{\mathrm{2}\left({a}−\mathrm{1}\right)}{\:\sqrt{{a}^{\mathrm{3}} }}{log}\left(\mathrm{1}−\sqrt{{ax}}\right)+{C} \\ $$

Answered by liberty last updated on 27/Dec/20

I=∫ (((√a)−(√x))/(1−(√(ax)))) dx ; take w=1−(√(ax)) dx = −((2(1−w))/a) dw I=∫ (((√a)−((1−w)/( (√a))))/w) (−((2(1−w))/a))dw I= −(2/(a(√a))) ∫ (((a−1)/w)+(2−a)−w)dw I=−(2/(a(√a))) [ (a−1)ln w +(2−a)w−(w^2 /2) ]+c I= (1/(a(√a))) [ 2(1−a)(√(ax)) + ax−2(a−1)ln (1−(√(ax)) )] + c

$${I}=\int\:\frac{\sqrt{{a}}−\sqrt{{x}}}{\mathrm{1}−\sqrt{{ax}}}\:{dx}\:;\:{take}\:{w}=\mathrm{1}−\sqrt{{ax}} \\ $$$$\:\:\:{dx}\:=\:−\frac{\mathrm{2}\left(\mathrm{1}−{w}\right)}{{a}}\:{dw} \\ $$$${I}=\int\:\frac{\sqrt{{a}}−\frac{\mathrm{1}−{w}}{\:\sqrt{{a}}}}{{w}}\:\left(−\frac{\mathrm{2}\left(\mathrm{1}−{w}\right)}{{a}}\right){dw} \\ $$$${I}=\:−\frac{\mathrm{2}}{{a}\sqrt{{a}}}\:\int\:\left(\frac{{a}−\mathrm{1}}{{w}}+\left(\mathrm{2}−{a}\right)−{w}\right){dw} \\ $$$${I}=−\frac{\mathrm{2}}{{a}\sqrt{{a}}}\:\left[\:\left({a}−\mathrm{1}\right)\mathrm{ln}\:{w}\:+\left(\mathrm{2}−{a}\right){w}−\frac{{w}^{\mathrm{2}} }{\mathrm{2}}\:\right]+{c} \\ $$$${I}=\:\frac{\mathrm{1}}{{a}\sqrt{{a}}}\:\left[\:\mathrm{2}\left(\mathrm{1}−{a}\right)\sqrt{{ax}}\:+\:{ax}−\mathrm{2}\left({a}−\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{1}−\sqrt{{ax}}\:\right)\right]\:+\:{c} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply