Menu Close

a-x-2-b-x-1-4-9-4a-b-2-

Tinku Tara 0 Comments
Pin




Question Number 167489 by mathlove last updated on 18/Mar/22
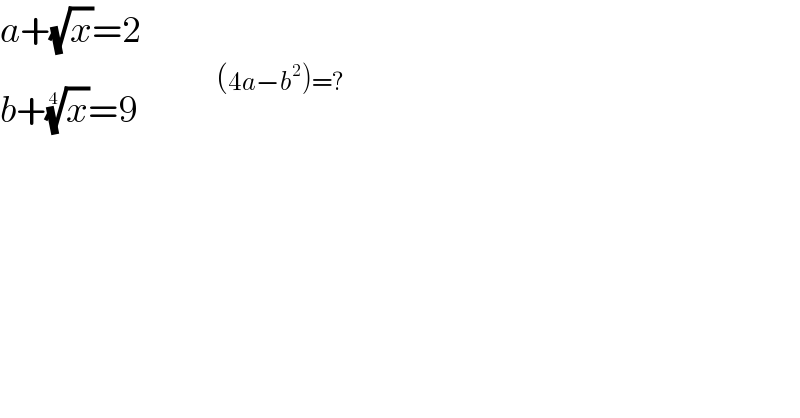
a+(√x)=2 b+(x)^(1/4) =9 ^( (4a−b^2 )=?)
$${a}+\sqrt{{x}}=\mathrm{2} \\ $$$${b}+\sqrt[{\mathrm{4}}]{{x}}=\mathrm{9}\:\:\:\:\:\:\:\:\:\overset{\:\:\:\:\:\:\left(\mathrm{4}{a}−{b}^{\mathrm{2}} \right)=?} {\:} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Mar/22
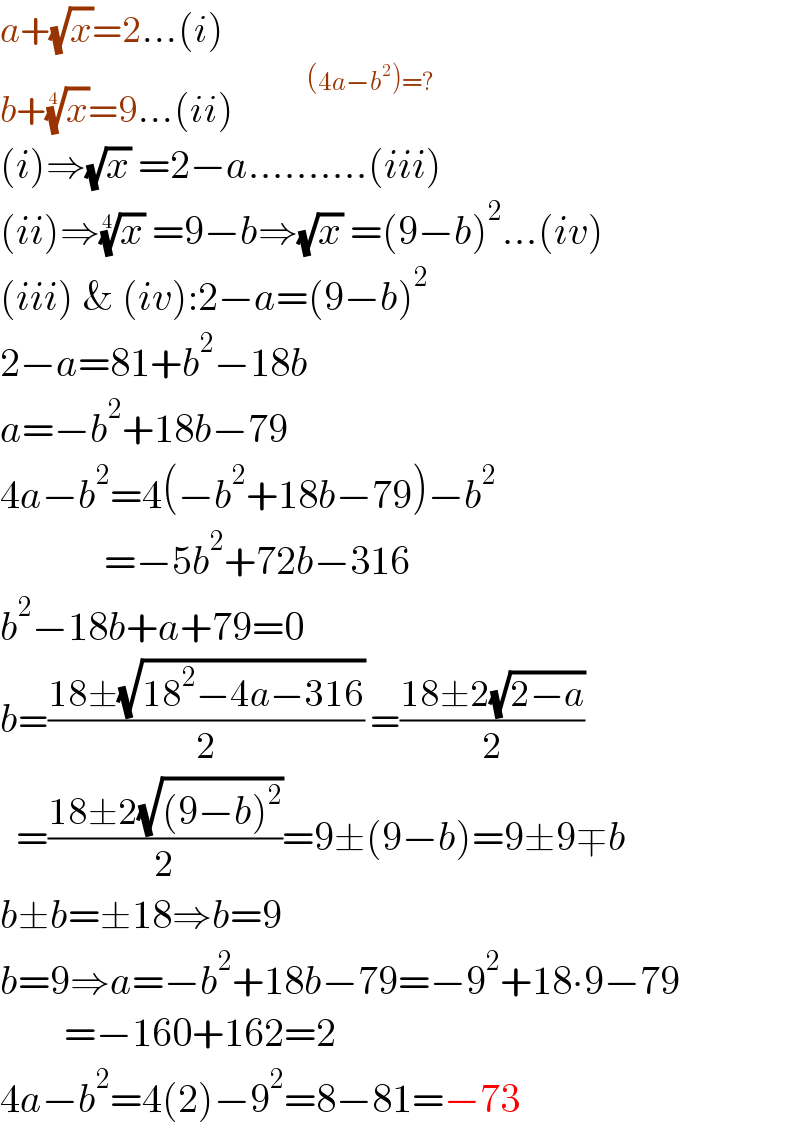
a+(√x)=2...(i) b+(x)^(1/4) =9...(ii) ^( (4a−b^2 )=?) (i)⇒(√x) =2−a..........(iii) (ii)⇒(x)^(1/4) =9−b⇒(√x) =(9−b)^2 ...(iv) (iii) & (iv):2−a=(9−b)^2 2−a=81+b^2 −18b a=−b^2 +18b−79 4a−b^2 =4(−b^2 +18b−79)−b^2 =−5b^2 +72b−316 b^2 −18b+a+79=0 b=((18±(√(18^2 −4a−316)))/2) =((18±2(√(2−a)))/2) =((18±2(√((9−b)^2 )))/2)=9±(9−b)=9±9∓b b±b=±18⇒b=9 b=9⇒a=−b^2 +18b−79=−9^2 +18∙9−79 =−160+162=2 4a−b^2 =4(2)−9^2 =8−81=−73
$${a}+\sqrt{{x}}=\mathrm{2}…\left({i}\right) \\ $$$${b}+\sqrt[{\mathrm{4}}]{{x}}=\mathrm{9}…\left({ii}\right)\:\:\:\:\:\:\:\:\overset{\:\:\:\:\:\:\left(\mathrm{4}{a}−{b}^{\mathrm{2}} \right)=?} {\:} \\ $$$$\left({i}\right)\Rightarrow\sqrt{{x}}\:=\mathrm{2}−{a}……….\left({iii}\right) \\ $$$$\left({ii}\right)\Rightarrow\sqrt[{\mathrm{4}}]{{x}}\:=\mathrm{9}−{b}\Rightarrow\sqrt{{x}}\:=\left(\mathrm{9}−{b}\right)^{\mathrm{2}} …\left({iv}\right) \\ $$$$\left({iii}\right)\:\&\:\left({iv}\right):\mathrm{2}−{a}=\left(\mathrm{9}−{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}−{a}=\mathrm{81}+{b}^{\mathrm{2}} −\mathrm{18}{b} \\ $$$${a}=−{b}^{\mathrm{2}} +\mathrm{18}{b}−\mathrm{79} \\ $$$$\mathrm{4}{a}−{b}^{\mathrm{2}} =\mathrm{4}\left(−{b}^{\mathrm{2}} +\mathrm{18}{b}−\mathrm{79}\right)−{b}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{5}{b}^{\mathrm{2}} +\mathrm{72}{b}−\mathrm{316} \\ $$$${b}^{\mathrm{2}} −\mathrm{18}{b}+{a}+\mathrm{79}=\mathrm{0} \\ $$$${b}=\frac{\mathrm{18}\pm\sqrt{\mathrm{18}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{316}}}{\mathrm{2}}\:=\frac{\mathrm{18}\pm\mathrm{2}\sqrt{\mathrm{2}−{a}}}{\mathrm{2}} \\ $$$$\:\:=\frac{\mathrm{18}\pm\mathrm{2}\sqrt{\left(\mathrm{9}−{b}\right)^{\mathrm{2}} }}{\mathrm{2}}=\mathrm{9}\pm\left(\mathrm{9}−{b}\right)=\mathrm{9}\pm\mathrm{9}\mp{b} \\ $$$${b}\pm{b}=\pm\mathrm{18}\Rightarrow{b}=\mathrm{9} \\ $$$${b}=\mathrm{9}\Rightarrow{a}=−{b}^{\mathrm{2}} +\mathrm{18}{b}−\mathrm{79}=−\mathrm{9}^{\mathrm{2}} +\mathrm{18}\centerdot\mathrm{9}−\mathrm{79} \\ $$$$\:\:\:\:\:\:\:\:=−\mathrm{160}+\mathrm{162}=\mathrm{2} \\ $$$$\mathrm{4}{a}−{b}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{2}\right)−\mathrm{9}^{\mathrm{2}} =\mathrm{8}−\mathrm{81}=−\mathrm{73} \\ $$
Commented by mathlove last updated on 18/Mar/22
thanks bro
$${thanks}\:{bro} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *