Question Number 47966 by ajfour last updated on 17/Nov/18
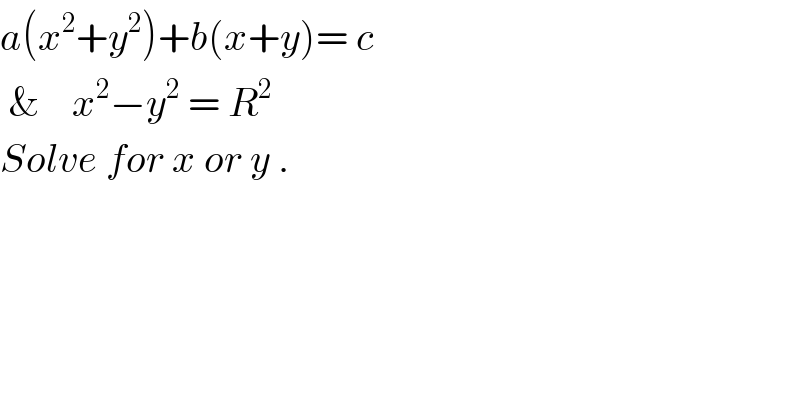
$${a}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+{b}\left({x}+{y}\right)=\:{c} \\ $$$$\:\&\:\:\:\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:=\:{R}^{\mathrm{2}} \\ $$$${Solve}\:{for}\:{x}\:{or}\:{y}\:. \\ $$
Commented by behi83417@gmail.com last updated on 17/Nov/18
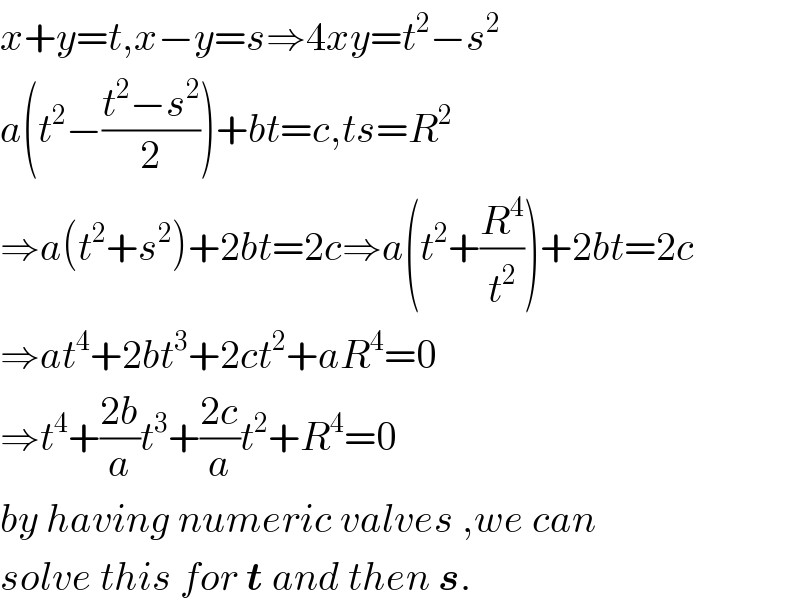
$${x}+{y}={t},{x}−{y}={s}\Rightarrow\mathrm{4}{xy}={t}^{\mathrm{2}} −{s}^{\mathrm{2}} \\ $$$${a}\left({t}^{\mathrm{2}} −\frac{{t}^{\mathrm{2}} −{s}^{\mathrm{2}} }{\mathrm{2}}\right)+{bt}={c},{ts}={R}^{\mathrm{2}} \\ $$$$\Rightarrow{a}\left({t}^{\mathrm{2}} +{s}^{\mathrm{2}} \right)+\mathrm{2}{bt}=\mathrm{2}{c}\Rightarrow{a}\left({t}^{\mathrm{2}} +\frac{{R}^{\mathrm{4}} }{{t}^{\mathrm{2}} }\right)+\mathrm{2}{bt}=\mathrm{2}{c} \\ $$$$\Rightarrow{at}^{\mathrm{4}} +\mathrm{2}{bt}^{\mathrm{3}} +\mathrm{2}{ct}^{\mathrm{2}} +{aR}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{4}} +\frac{\mathrm{2}{b}}{{a}}{t}^{\mathrm{3}} +\frac{\mathrm{2}{c}}{{a}}{t}^{\mathrm{2}} +{R}^{\mathrm{4}} =\mathrm{0} \\ $$$${by}\:{having}\:{numeric}\:{valves}\:,{we}\:{can} \\ $$$${solve}\:{this}\:{for}\:\boldsymbol{{t}}\:{and}\:{then}\:\boldsymbol{{s}}. \\ $$
Answered by MJS last updated on 17/Nov/18
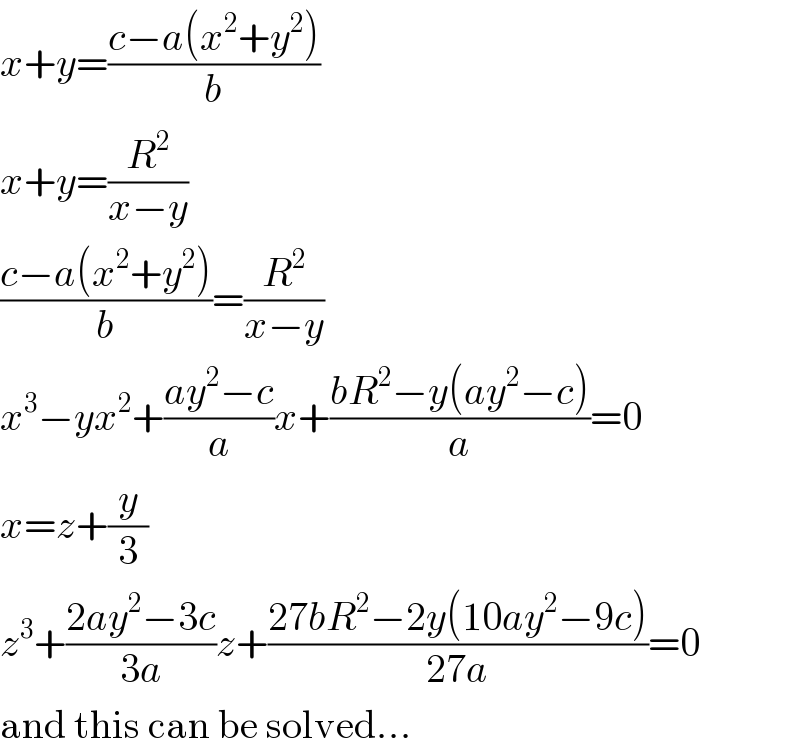
$${x}+{y}=\frac{{c}−{a}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}{{b}} \\ $$$${x}+{y}=\frac{{R}^{\mathrm{2}} }{{x}−{y}} \\ $$$$\frac{{c}−{a}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}{{b}}=\frac{{R}^{\mathrm{2}} }{{x}−{y}} \\ $$$${x}^{\mathrm{3}} −{yx}^{\mathrm{2}} +\frac{{ay}^{\mathrm{2}} −{c}}{{a}}{x}+\frac{{bR}^{\mathrm{2}} −{y}\left({ay}^{\mathrm{2}} −{c}\right)}{{a}}=\mathrm{0} \\ $$$${x}={z}+\frac{{y}}{\mathrm{3}} \\ $$$${z}^{\mathrm{3}} +\frac{\mathrm{2}{ay}^{\mathrm{2}} −\mathrm{3}{c}}{\mathrm{3}{a}}{z}+\frac{\mathrm{27}{bR}^{\mathrm{2}} −\mathrm{2}{y}\left(\mathrm{10}{ay}^{\mathrm{2}} −\mathrm{9}{c}\right)}{\mathrm{27}{a}}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}… \\ $$
