Question Number 146764 by Ar Brandon last updated on 15/Jul/21
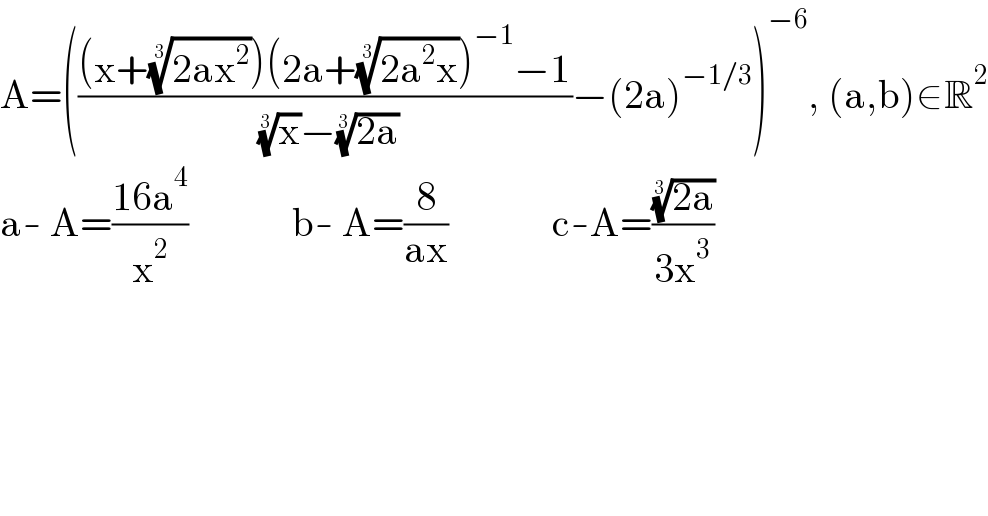
$$\mathrm{A}=\left(\frac{\left(\mathrm{x}+\sqrt[{\mathrm{3}}]{\mathrm{2ax}^{\mathrm{2}} }\right)\left(\mathrm{2a}+\sqrt[{\mathrm{3}}]{\mathrm{2a}^{\mathrm{2}} \mathrm{x}}\right)^{−\mathrm{1}} −\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{x}}−\sqrt[{\mathrm{3}}]{\mathrm{2a}}}−\left(\mathrm{2a}\right)^{−\mathrm{1}/\mathrm{3}} \right)^{−\mathrm{6}} ,\:\left(\mathrm{a},\mathrm{b}\right)\in\mathbb{R}^{\mathrm{2}} \\ $$$$\mathrm{a}-\:\mathrm{A}=\frac{\mathrm{16a}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}-\:\mathrm{A}=\frac{\mathrm{8}}{\mathrm{ax}}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{c}-\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2a}}}{\mathrm{3x}^{\mathrm{3}} } \\ $$
