Question Number 62275 by behi83417@gmail.com last updated on 18/Jun/19
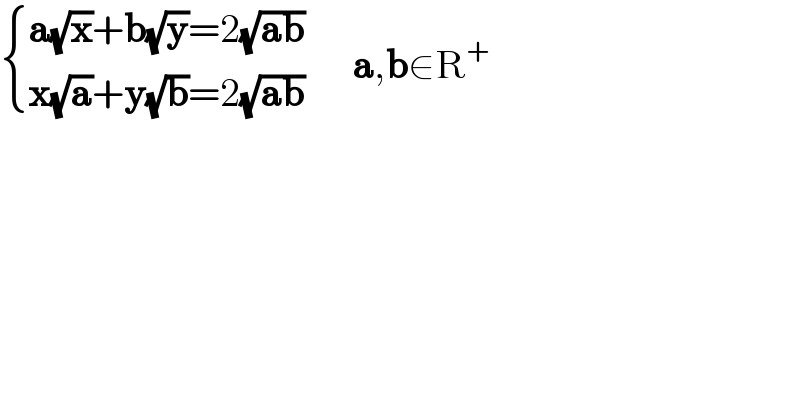
$$\begin{cases}{\boldsymbol{\mathrm{a}}\sqrt{\boldsymbol{\mathrm{x}}}+\boldsymbol{\mathrm{b}}\sqrt{\boldsymbol{\mathrm{y}}}=\mathrm{2}\sqrt{\boldsymbol{\mathrm{ab}}}}\\{\boldsymbol{\mathrm{x}}\sqrt{\boldsymbol{\mathrm{a}}}+\boldsymbol{\mathrm{y}}\sqrt{\boldsymbol{\mathrm{b}}}=\mathrm{2}\sqrt{\boldsymbol{\mathrm{ab}}}}\end{cases}\:\:\:\:\:\:\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}\in\mathrm{R}^{+} \\ $$
Answered by mr W last updated on 19/Jun/19
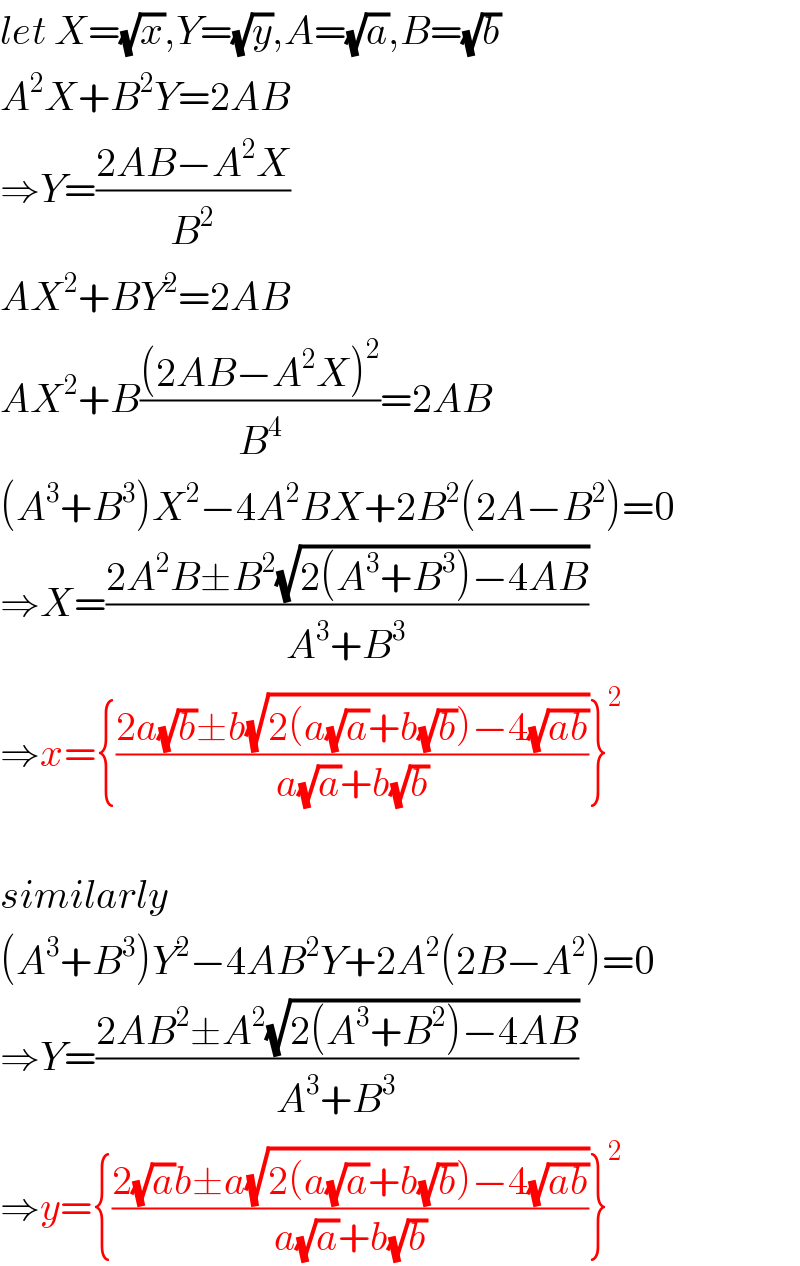
$${let}\:{X}=\sqrt{{x}},{Y}=\sqrt{{y}},{A}=\sqrt{{a}},{B}=\sqrt{{b}} \\ $$$${A}^{\mathrm{2}} {X}+{B}^{\mathrm{2}} {Y}=\mathrm{2}{AB} \\ $$$$\Rightarrow{Y}=\frac{\mathrm{2}{AB}−{A}^{\mathrm{2}} {X}}{{B}^{\mathrm{2}} } \\ $$$${AX}^{\mathrm{2}} +{BY}^{\mathrm{2}} =\mathrm{2}{AB} \\ $$$${AX}^{\mathrm{2}} +{B}\frac{\left(\mathrm{2}{AB}−{A}^{\mathrm{2}} {X}\right)^{\mathrm{2}} }{{B}^{\mathrm{4}} }=\mathrm{2}{AB} \\ $$$$\left({A}^{\mathrm{3}} +{B}^{\mathrm{3}} \right){X}^{\mathrm{2}} −\mathrm{4}{A}^{\mathrm{2}} {BX}+\mathrm{2}{B}^{\mathrm{2}} \left(\mathrm{2}{A}−{B}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{X}=\frac{\mathrm{2}{A}^{\mathrm{2}} {B}\pm{B}^{\mathrm{2}} \sqrt{\mathrm{2}\left({A}^{\mathrm{3}} +{B}^{\mathrm{3}} \right)−\mathrm{4}{AB}}}{{A}^{\mathrm{3}} +{B}^{\mathrm{3}} } \\ $$$$\Rightarrow{x}=\left\{\frac{\mathrm{2}{a}\sqrt{{b}}\pm{b}\sqrt{\mathrm{2}\left({a}\sqrt{{a}}+{b}\sqrt{{b}}\right)−\mathrm{4}\sqrt{{ab}}}}{{a}\sqrt{{a}}+{b}\sqrt{{b}}}\right\}^{\mathrm{2}} \\ $$$$ \\ $$$${similarly} \\ $$$$\left({A}^{\mathrm{3}} +{B}^{\mathrm{3}} \right){Y}^{\mathrm{2}} −\mathrm{4}{AB}^{\mathrm{2}} {Y}+\mathrm{2}{A}^{\mathrm{2}} \left(\mathrm{2}{B}−{A}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{Y}=\frac{\mathrm{2}{AB}^{\mathrm{2}} \pm{A}^{\mathrm{2}} \sqrt{\mathrm{2}\left({A}^{\mathrm{3}} +{B}^{\mathrm{2}} \right)−\mathrm{4}{AB}}}{{A}^{\mathrm{3}} +{B}^{\mathrm{3}} } \\ $$$$\Rightarrow{y}=\left\{\frac{\mathrm{2}\sqrt{{a}}{b}\pm{a}\sqrt{\mathrm{2}\left({a}\sqrt{{a}}+{b}\sqrt{{b}}\right)−\mathrm{4}\sqrt{{ab}}}}{{a}\sqrt{{a}}+{b}\sqrt{{b}}}\right\}^{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 20/Jun/19

$$\mathrm{perfect}\:\mathrm{sir}.\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{master}. \\ $$
