Menu Close

abc-8-a-b-c-7-a-3-b-3-c-3-73-then-faind-the-vole-of-1-a-1-b-1-c-

Tinku Tara 0 Comments
Pin




Question Number 161947 by mathlove last updated on 24/Dec/21
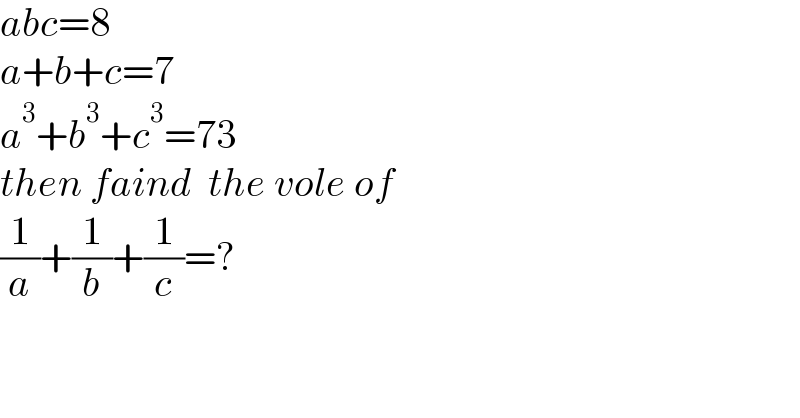
abc=8 a+b+c=7 a^3 +b^3 +c^3 =73 then faind the vole of (1/a)+(1/b)+(1/c)=?
$${abc}=\mathrm{8} \\ $$$${a}+{b}+{c}=\mathrm{7} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{73} \\ $$$${then}\:{faind}\:\:{the}\:{vole}\:{of} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=? \\ $$
Answered by Rasheed.Sindhi last updated on 24/Dec/21
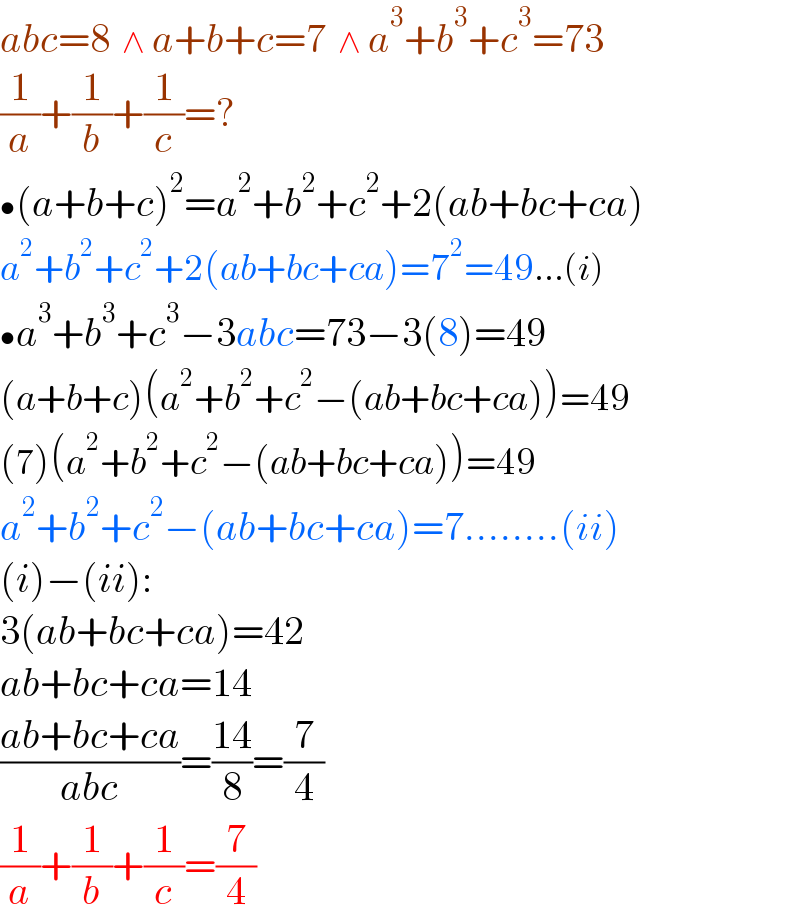
abc=8 ∧ a+b+c=7 ∧ a^3 +b^3 +c^3 =73 (1/a)+(1/b)+(1/c)=? •(a+b+c)^2 =a^2 +b^2 +c^2 +2(ab+bc+ca) a^2 +b^2 +c^2 +2(ab+bc+ca)=7^2 =49...(i) •a^3 +b^3 +c^3 −3abc=73−3(8)=49 (a+b+c)(a^2 +b^2 +c^2 −(ab+bc+ca))=49 (7)(a^2 +b^2 +c^2 −(ab+bc+ca))=49 a^2 +b^2 +c^2 −(ab+bc+ca)=7........(ii) (i)−(ii): 3(ab+bc+ca)=42 ab+bc+ca=14 ((ab+bc+ca)/(abc))=((14)/8)=(7/4) (1/a)+(1/b)+(1/c)=(7/4)
$${abc}=\mathrm{8}\:\:\wedge\:{a}+{b}+{c}=\mathrm{7}\:\:\wedge\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{73} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=? \\ $$$$\bullet\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right)=\mathrm{7}^{\mathrm{2}} =\mathrm{49}…\left({i}\right) \\ $$$$\bullet{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}=\mathrm{73}−\mathrm{3}\left(\mathrm{8}\right)=\mathrm{49} \\ $$$$\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{bc}+{ca}\right)\right)=\mathrm{49} \\ $$$$\left(\mathrm{7}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{bc}+{ca}\right)\right)=\mathrm{49} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{bc}+{ca}\right)=\mathrm{7}……..\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\mathrm{3}\left({ab}+{bc}+{ca}\right)=\mathrm{42} \\ $$$${ab}+{bc}+{ca}=\mathrm{14} \\ $$$$\frac{{ab}+{bc}+{ca}}{{abc}}=\frac{\mathrm{14}}{\mathrm{8}}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$
Answered by mr W last updated on 24/Dec/21
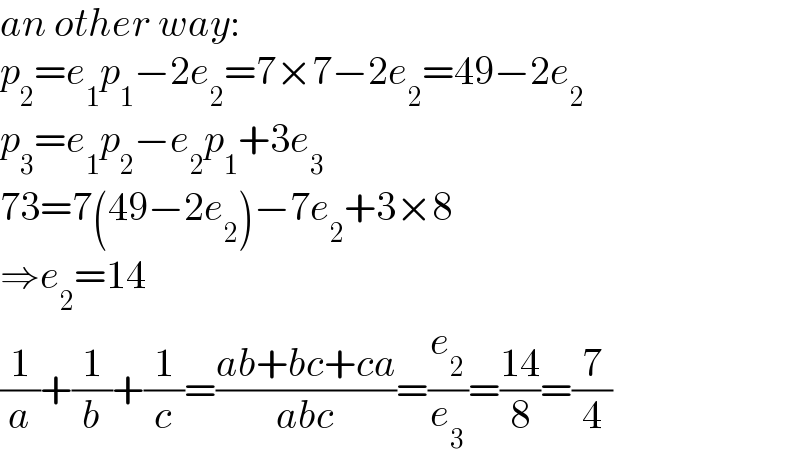
an other way: p_2 =e_1 p_1 −2e_2 =7×7−2e_2 =49−2e_2 p_3 =e_1 p_2 −e_2 p_1 +3e_3 73=7(49−2e_2 )−7e_2 +3×8 ⇒e_2 =14 (1/a)+(1/b)+(1/c)=((ab+bc+ca)/(abc))=(e_2 /e_3 )=((14)/8)=(7/4)
$${an}\:{other}\:{way}: \\ $$$${p}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} =\mathrm{7}×\mathrm{7}−\mathrm{2}{e}_{\mathrm{2}} =\mathrm{49}−\mathrm{2}{e}_{\mathrm{2}} \\ $$$${p}_{\mathrm{3}} ={e}_{\mathrm{1}} {p}_{\mathrm{2}} −{e}_{\mathrm{2}} {p}_{\mathrm{1}} +\mathrm{3}{e}_{\mathrm{3}} \\ $$$$\mathrm{73}=\mathrm{7}\left(\mathrm{49}−\mathrm{2}{e}_{\mathrm{2}} \right)−\mathrm{7}{e}_{\mathrm{2}} +\mathrm{3}×\mathrm{8} \\ $$$$\Rightarrow{e}_{\mathrm{2}} =\mathrm{14} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{{ab}+{bc}+{ca}}{{abc}}=\frac{{e}_{\mathrm{2}} }{{e}_{\mathrm{3}} }=\frac{\mathrm{14}}{\mathrm{8}}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$
Commented by Tawa11 last updated on 24/Dec/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *