Menu Close

ABC-DEF-ABC-25-DEF-35-Madian-2-of-ABC-Madian-2-of-DEF-

Tinku Tara 0 Comments
Pin




Question Number 13434 by Nayon last updated on 20/May/17
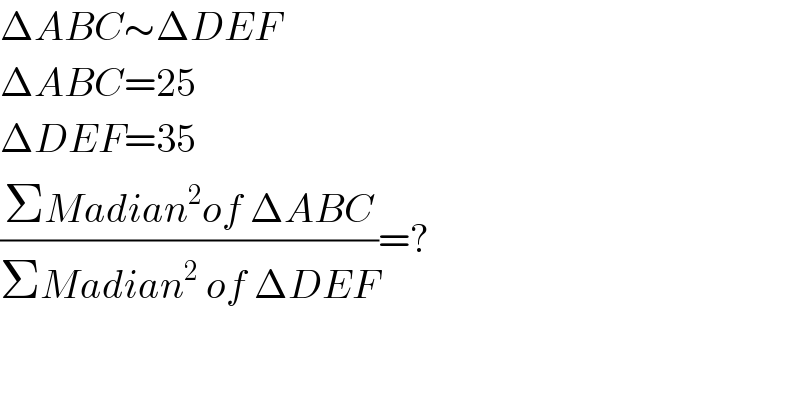
ΔABC∼ΔDEF ΔABC=25 ΔDEF=35 ((ΣMadian^2 of ΔABC)/(ΣMadian^2 of ΔDEF))=?
$$\Delta{ABC}\sim\Delta{DEF}\: \\ $$$$\Delta{ABC}=\mathrm{25} \\ $$$$\Delta{DEF}=\mathrm{35} \\ $$$$\frac{\Sigma{Madian}^{\mathrm{2}} {of}\:\Delta{ABC}}{\Sigma{Madian}^{\mathrm{2}} \:{of}\:\Delta{DEF}}=? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17
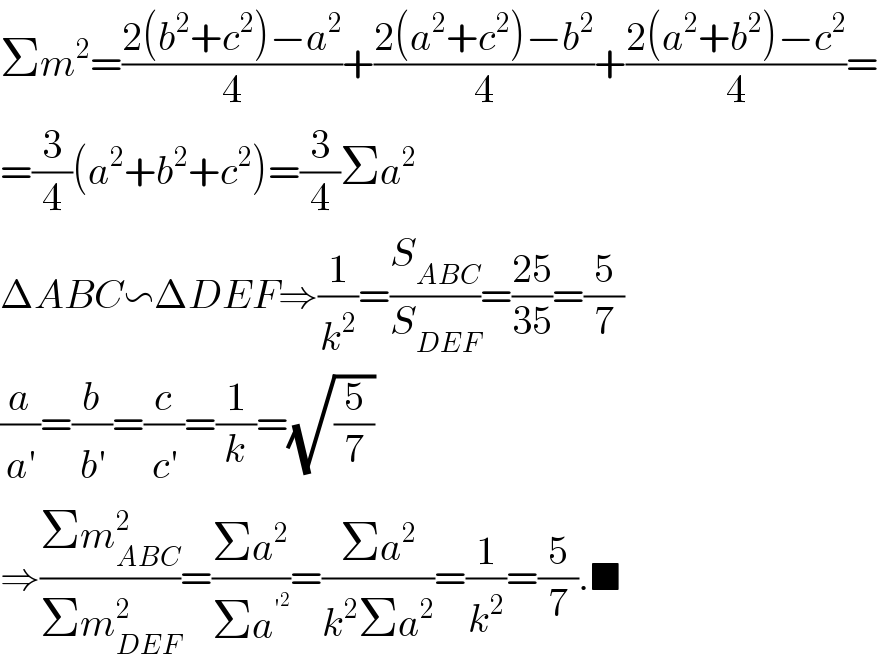
Σm^2 =((2(b^2 +c^2 )−a^2 )/4)+((2(a^2 +c^2 )−b^2 )/4)+((2(a^2 +b^2 )−c^2 )/4)= =(3/4)(a^2 +b^2 +c^2 )=(3/4)Σa^2 ΔABC∽ΔDEF⇒(1/k^2 )=(S_(ABC) /S_(DEF) )=((25)/(35))=(5/7) (a/a^′ )=(b/b^′ )=(c/c^′ )=(1/k)=(√(5/7)) ⇒((Σm_(ABC) ^2 )/(Σm_(DEF) ^2 ))=((Σa^2 )/(Σa^′^2 ))=((Σa^2 )/(k^2 Σa^2 ))=(1/k^2 )=(5/7).■
$$\Sigma{m}^{\mathrm{2}} =\frac{\mathrm{2}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} }{\mathrm{4}}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)=\frac{\mathrm{3}}{\mathrm{4}}\Sigma{a}^{\mathrm{2}} \\ $$$$\Delta{ABC}\backsim\Delta{DEF}\Rightarrow\frac{\mathrm{1}}{{k}^{\mathrm{2}} }=\frac{{S}_{{ABC}} }{{S}_{{DEF}} }=\frac{\mathrm{25}}{\mathrm{35}}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\frac{{a}}{{a}^{'} }=\frac{{b}}{{b}^{'} }=\frac{{c}}{{c}^{'} }=\frac{\mathrm{1}}{{k}}=\sqrt{\frac{\mathrm{5}}{\mathrm{7}}} \\ $$$$\Rightarrow\frac{\Sigma{m}_{{ABC}} ^{\mathrm{2}} }{\Sigma{m}_{{DEF}} ^{\mathrm{2}} }=\frac{\Sigma{a}^{\mathrm{2}} }{\Sigma{a}^{'^{\mathrm{2}} } }=\frac{\Sigma{a}^{\mathrm{2}} }{{k}^{\mathrm{2}} \Sigma{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{{k}^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{7}}.\blacksquare \\ $$
Answered by mrW1 last updated on 20/May/17
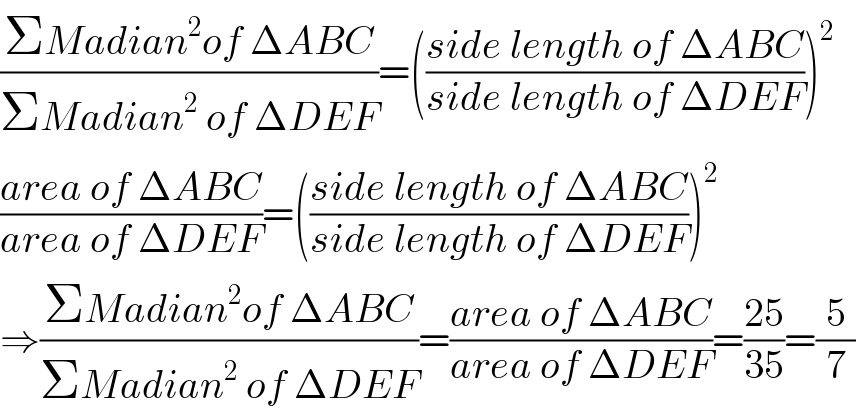
((ΣMadian^2 of ΔABC)/(ΣMadian^2 of ΔDEF))=(((side length of ΔABC)/(side length of ΔDEF)))^2 ((area of ΔABC)/(area of ΔDEF))=(((side length of ΔABC)/(side length of ΔDEF)))^2 ⇒((ΣMadian^2 of ΔABC)/(ΣMadian^2 of ΔDEF))=((area of ΔABC)/(area of ΔDEF))=((25)/(35))=(5/7)
$$\frac{\Sigma{Madian}^{\mathrm{2}} {of}\:\Delta{ABC}}{\Sigma{Madian}^{\mathrm{2}} \:{of}\:\Delta{DEF}}=\left(\frac{{side}\:{length}\:{of}\:\Delta{ABC}}{{side}\:{length}\:{of}\:\Delta{DEF}}\right)^{\mathrm{2}} \\ $$$$\frac{{area}\:{of}\:\Delta{ABC}}{{area}\:{of}\:\Delta{DEF}}=\left(\frac{{side}\:{length}\:{of}\:\Delta{ABC}}{{side}\:{length}\:{of}\:\Delta{DEF}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\Sigma{Madian}^{\mathrm{2}} {of}\:\Delta{ABC}}{\Sigma{Madian}^{\mathrm{2}} \:{of}\:\Delta{DEF}}=\frac{{area}\:{of}\:\Delta{ABC}}{{area}\:{of}\:\Delta{DEF}}=\frac{\mathrm{25}}{\mathrm{35}}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *