Question Number 125758 by ZiYangLee last updated on 13/Dec/20

$$\Delta\mathrm{ABC}\:\mathrm{have}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{length}\:\mathrm{10}\:\mathrm{13}\:\mathrm{13} \\ $$$$\mathrm{while}\:\Delta\mathrm{PQR}\:\mathrm{have}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{length} \\ $$$$\mathrm{13}\:\mathrm{13}\:\mathrm{24}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{Area}\:\mathrm{of}\:\Delta\mathrm{ABC}\::\:\mathrm{Area} \\ $$$$\mathrm{of}\:\Delta\mathrm{PQR}. \\ $$
Answered by mr W last updated on 13/Dec/20
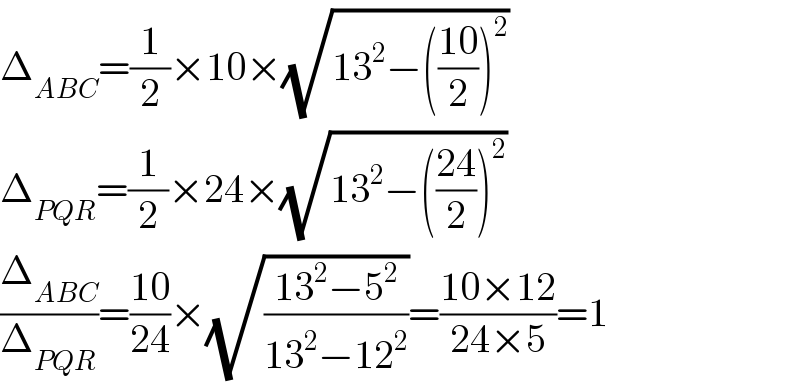
$$\Delta_{{ABC}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{10}×\sqrt{\mathrm{13}^{\mathrm{2}} −\left(\frac{\mathrm{10}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\Delta_{{PQR}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{24}×\sqrt{\mathrm{13}^{\mathrm{2}} −\left(\frac{\mathrm{24}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\frac{\Delta_{{ABC}} }{\Delta_{{PQR}} }=\frac{\mathrm{10}}{\mathrm{24}}×\sqrt{\frac{\mathrm{13}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{13}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} }}=\frac{\mathrm{10}×\mathrm{12}}{\mathrm{24}×\mathrm{5}}=\mathrm{1} \\ $$
Answered by MJS_new last updated on 13/Dec/20
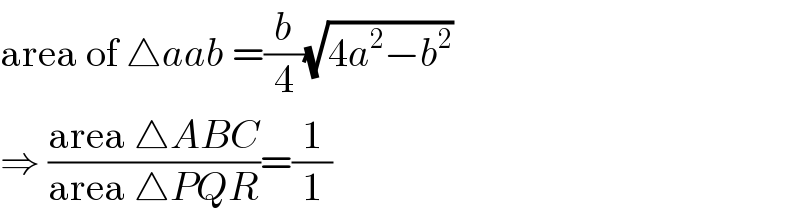
$$\mathrm{area}\:\mathrm{of}\:\bigtriangleup{aab}\:=\frac{{b}}{\mathrm{4}}\sqrt{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\mathrm{area}\:\bigtriangleup{ABC}}{\mathrm{area}\:\bigtriangleup{PQR}}=\frac{\mathrm{1}}{\mathrm{1}} \\ $$
