Menu Close

ABC-is-a-triangle-prove-that-sinA-sinB-sinC-gt-sinA-sinB-sinC-

Tinku Tara 0 Comments
Pin




Question Number 84849 by M±th+et£s last updated on 16/Mar/20
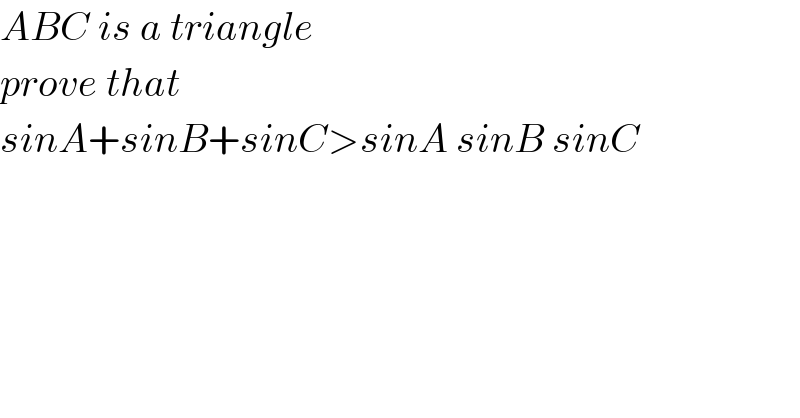
ABC is a triangle prove that sinA+sinB+sinC>sinA sinB sinC
$${ABC}\:{is}\:{a}\:{triangle}\: \\ $$$${prove}\:{that} \\ $$$${sinA}+{sinB}+{sinC}>{sinA}\:{sinB}\:{sinC} \\ $$
Commented by ajfour last updated on 16/Mar/20
0< sin A , sin B, sin C ≤ 1 so it should be obvious.
$$\mathrm{0}<\:\mathrm{sin}\:{A}\:,\:\mathrm{sin}\:{B},\:\mathrm{sin}\:{C}\:\leqslant\:\mathrm{1} \\ $$$${so}\:{it}\:{should}\:{be}\:{obvious}. \\ $$
Commented by M±th+et£s last updated on 16/Mar/20
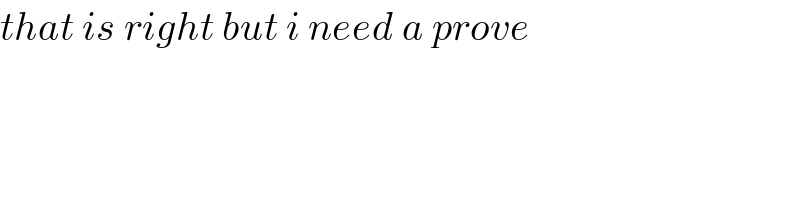
that is right but i need a prove
$${that}\:{is}\:{right}\:{but}\:{i}\:{need}\:{a}\:{prove} \\ $$
Commented by MJS last updated on 17/Mar/20
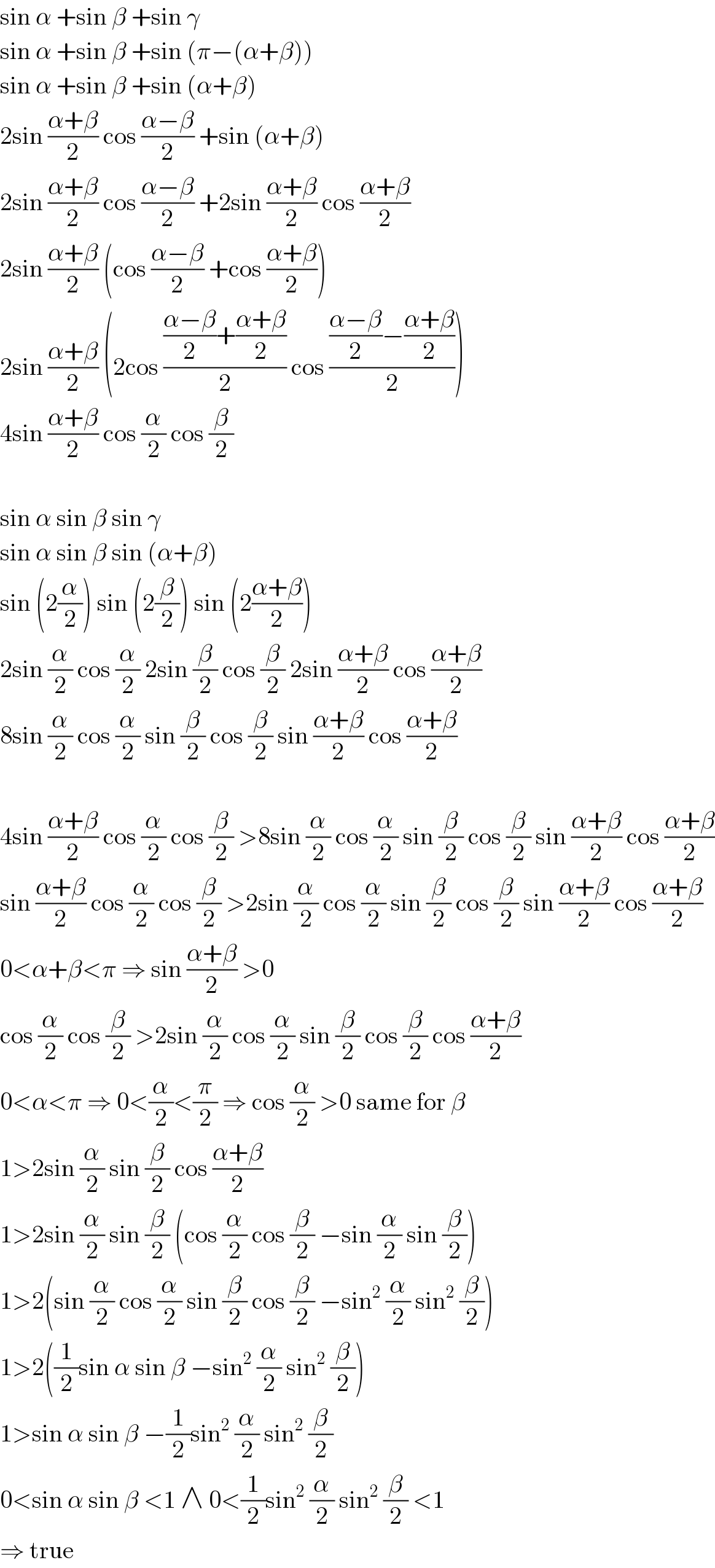
sin α +sin β +sin γ sin α +sin β +sin (π−(α+β)) sin α +sin β +sin (α+β) 2sin ((α+β)/2) cos ((α−β)/2) +sin (α+β) 2sin ((α+β)/2) cos ((α−β)/2) +2sin ((α+β)/2) cos ((α+β)/2) 2sin ((α+β)/2) (cos ((α−β)/2) +cos ((α+β)/2)) 2sin ((α+β)/2) (2cos ((((α−β)/2)+((α+β)/2))/2) cos ((((α−β)/2)−((α+β)/2))/2)) 4sin ((α+β)/2) cos (α/2) cos (β/2) sin α sin β sin γ sin α sin β sin (α+β) sin (2(α/2)) sin (2(β/2)) sin (2((α+β)/2)) 2sin (α/2) cos (α/2) 2sin (β/2) cos (β/2) 2sin ((α+β)/2) cos ((α+β)/2) 8sin (α/2) cos (α/2) sin (β/2) cos (β/2) sin ((α+β)/2) cos ((α+β)/2) 4sin ((α+β)/2) cos (α/2) cos (β/2) >8sin (α/2) cos (α/2) sin (β/2) cos (β/2) sin ((α+β)/2) cos ((α+β)/2) sin ((α+β)/2) cos (α/2) cos (β/2) >2sin (α/2) cos (α/2) sin (β/2) cos (β/2) sin ((α+β)/2) cos ((α+β)/2) 0<α+β<π ⇒ sin ((α+β)/2) >0 cos (α/2) cos (β/2) >2sin (α/2) cos (α/2) sin (β/2) cos (β/2) cos ((α+β)/2) 0<α<π ⇒ 0<(α/2)<(π/2) ⇒ cos (α/2) >0 same for β 1>2sin (α/2) sin (β/2) cos ((α+β)/2) 1>2sin (α/2) sin (β/2) (cos (α/2) cos (β/2) −sin (α/2) sin (β/2)) 1>2(sin (α/2) cos (α/2) sin (β/2) cos (β/2) −sin^2 (α/2) sin^2 (β/2)) 1>2((1/2)sin α sin β −sin^2 (α/2) sin^2 (β/2)) 1>sin α sin β −(1/2)sin^2 (α/2) sin^2 (β/2) 0<sin α sin β <1 ∧ 0<(1/2)sin^2 (α/2) sin^2 (β/2) <1 ⇒ true
$$\mathrm{sin}\:\alpha\:+\mathrm{sin}\:\beta\:+\mathrm{sin}\:\gamma \\ $$$$\mathrm{sin}\:\alpha\:+\mathrm{sin}\:\beta\:+\mathrm{sin}\:\left(\pi−\left(\alpha+\beta\right)\right) \\ $$$$\mathrm{sin}\:\alpha\:+\mathrm{sin}\:\beta\:+\mathrm{sin}\:\left(\alpha+\beta\right) \\ $$$$\mathrm{2sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}\:+\mathrm{sin}\:\left(\alpha+\beta\right) \\ $$$$\mathrm{2sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}\:+\mathrm{2sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\mathrm{2sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\left(\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}\:+\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}}\right) \\ $$$$\mathrm{2sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\left(\mathrm{2cos}\:\frac{\frac{\alpha−\beta}{\mathrm{2}}+\frac{\alpha+\beta}{\mathrm{2}}}{\mathrm{2}}\:\mathrm{cos}\:\frac{\frac{\alpha−\beta}{\mathrm{2}}−\frac{\alpha+\beta}{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$\mathrm{4sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:\mathrm{sin}\:\gamma \\ $$$$\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:\mathrm{sin}\:\left(\alpha+\beta\right) \\ $$$$\mathrm{sin}\:\left(\mathrm{2}\frac{\alpha}{\mathrm{2}}\right)\:\mathrm{sin}\:\left(\mathrm{2}\frac{\beta}{\mathrm{2}}\right)\:\mathrm{sin}\:\left(\mathrm{2}\frac{\alpha+\beta}{\mathrm{2}}\right) \\ $$$$\mathrm{2sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{2sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{2sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\mathrm{8sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{4sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:>\mathrm{8sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:>\mathrm{2sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\mathrm{0}<\alpha+\beta<\pi\:\Rightarrow\:\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}}\:>\mathrm{0} \\ $$$$\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:>\mathrm{2sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\mathrm{0}<\alpha<\pi\:\Rightarrow\:\mathrm{0}<\frac{\alpha}{\mathrm{2}}<\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:>\mathrm{0}\:\mathrm{same}\:\mathrm{for}\:\beta \\ $$$$\mathrm{1}>\mathrm{2sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\mathrm{1}>\mathrm{2sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\left(\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:−\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\right) \\ $$$$\mathrm{1}>\mathrm{2}\left(\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:−\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\beta}{\mathrm{2}}\right) \\ $$$$\mathrm{1}>\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:−\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\beta}{\mathrm{2}}\right) \\ $$$$\mathrm{1}>\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\beta}{\mathrm{2}} \\ $$$$\mathrm{0}<\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:<\mathrm{1}\:\wedge\:\mathrm{0}<\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\beta}{\mathrm{2}}\:<\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{true} \\ $$
Commented by M±th+et£s last updated on 17/Mar/20
god bless you sir
$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by MJS last updated on 17/Mar/20
you′re welcome maybe there′s a shorter way, I just started trying and this is where it lead me...
$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$$$\mathrm{maybe}\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{shorter}\:\mathrm{way},\:\mathrm{I}\:\mathrm{just}\:\mathrm{started} \\ $$$$\mathrm{trying}\:\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{where}\:\mathrm{it}\:\mathrm{lead}\:\mathrm{me}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *