ABC-is-a-triangular-park-with-AB-AC-100-m-A-clock-tower-is-situated-at-the-midpoint-of-BC-The-angles-of-elevation-of-top-of-the-tower-at-A-and-B-are-cot-1-3-2-and-cosec-1-2-6-respectiv

Question Number 17647 by Tinkutara last updated on 09/Jul/17

$${ABC}\:\mathrm{is}\:\mathrm{a}\:\mathrm{triangular}\:\mathrm{park}\:\mathrm{with}\:{AB}\:= \\ $$$${AC}\:=\:\mathrm{100}\:\mathrm{m}.\:\mathrm{A}\:\mathrm{clock}\:\mathrm{tower}\:\mathrm{is}\:\mathrm{situated} \\ $$$$\mathrm{at}\:\mathrm{the}\:\mathrm{midpoint}\:\mathrm{of}\:{BC}.\:\mathrm{The}\:\mathrm{angles}\:\mathrm{of} \\ $$$$\mathrm{elevation}\:\mathrm{of}\:\mathrm{top}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tower}\:\mathrm{at}\:{A}\:\mathrm{and} \\ $$$${B}\:\mathrm{are}\:\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{3}.\mathrm{2}\right)\:\mathrm{and}\:\mathrm{cosec}^{−\mathrm{1}} \left(\mathrm{2}.\mathrm{6}\right) \\ $$$$\mathrm{respectively}.\:\mathrm{The}\:\mathrm{height}\:\mathrm{of}\:\mathrm{tower}\:\mathrm{is} \\ $$

Commented by ajfour last updated on 09/Jul/17

Commented by ajfour last updated on 09/Jul/17

∠AFB=90° because AB=AC and F is midpoint of BC. let HF=tower height ′ h′. BF^2 +AF^2 =AB^2 (hcot θ)^2 +(hcot φ)^2 =AB^2 h^2 = ((AB^2 )/(cot^2 θ+cot^2 φ)) = ((100×100m^2 )/((2.6)^2 −1+(3.2)^2 )) = ((100×100)/(16))m^2 ⇒ h=((100)/4)m =25m.

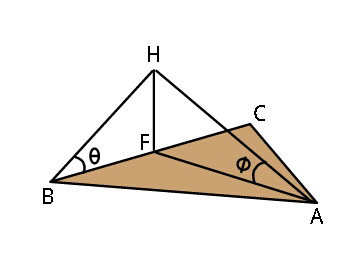
$$\angle\mathrm{AFB}=\mathrm{90}°\:\:\mathrm{because}\:\mathrm{AB}=\mathrm{AC} \\ $$$$\mathrm{and}\:\mathrm{F}\:\mathrm{is}\:\mathrm{midpoint}\:\mathrm{of}\:\mathrm{BC}. \\ $$$$\mathrm{let}\:\mathrm{HF}=\mathrm{tower}\:\mathrm{height}\:'\:\boldsymbol{\mathrm{h}}'. \\ $$$$\:\:\:\:\:\:\mathrm{BF}^{\mathrm{2}} +\mathrm{AF}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} \\ $$$$\:\:\:\:\left(\mathrm{hcot}\:\theta\right)^{\mathrm{2}} +\left(\mathrm{hcot}\:\phi\right)^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{h}^{\mathrm{2}} =\:\frac{\mathrm{AB}^{\mathrm{2}} }{\mathrm{cot}\:^{\mathrm{2}} \theta+\mathrm{cot}\:^{\mathrm{2}} \phi} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{100}×\mathrm{100m}^{\mathrm{2}} }{\left(\mathrm{2}.\mathrm{6}\right)^{\mathrm{2}} −\mathrm{1}+\left(\mathrm{3}.\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{100}×\mathrm{100}}{\mathrm{16}}\mathrm{m}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{h}=\frac{\mathrm{100}}{\mathrm{4}}\mathrm{m}\:=\mathrm{25m}. \\ $$

Commented by Tinkutara last updated on 09/Jul/17