Question Number 90456 by Tony Lin last updated on 23/Apr/20
$${ABCD}\:{is}\:{a}\:{square}\:{with}\:{side}\:{length}=\mathrm{1} \\ $$$${E}\:{is}\:{a}\:{moving}\:{point}\:{between}\:{B\&C} \\ $$$${F}\:{is}\:{a}\:{moving}\:{point}\:{between}\:{C\&D} \\ $$$${Find}\:{the}\:{maximum}\:{radius}\:{of}\:{inscribed} \\ $$$${circle}\:{in}\:\bigtriangleup{AEF} \\ $$
Answered by mr W last updated on 23/Apr/20
$${r}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{tan}\:\theta\right)\mathrm{tan}\:\left(\frac{\pi}{\mathrm{8}}+\frac{\theta}{\mathrm{2}}\right) \\ $$$${r}_{{max}} =\mathrm{0}.\mathrm{3032}\:{at}\:\theta=\mathrm{9}.\mathrm{3719}° \\ $$
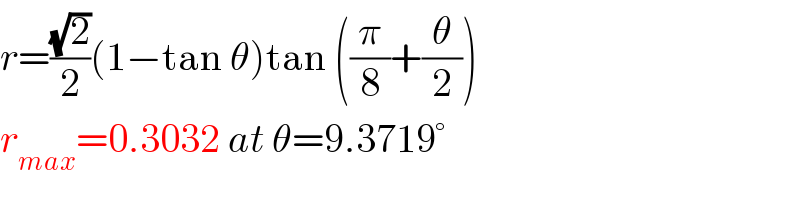
Commented by Tony Lin last updated on 24/Apr/20
$${Sir}\:{MrW},\:{could}\:{you}\:{please}\:{enumerate} \\ $$$${how}\:{to}\:{do}\:{it}? \\ $$
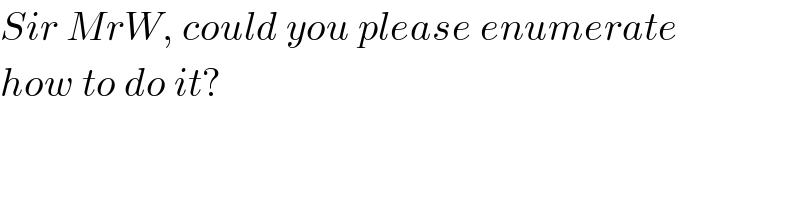
Answered by ajfour last updated on 24/Apr/20
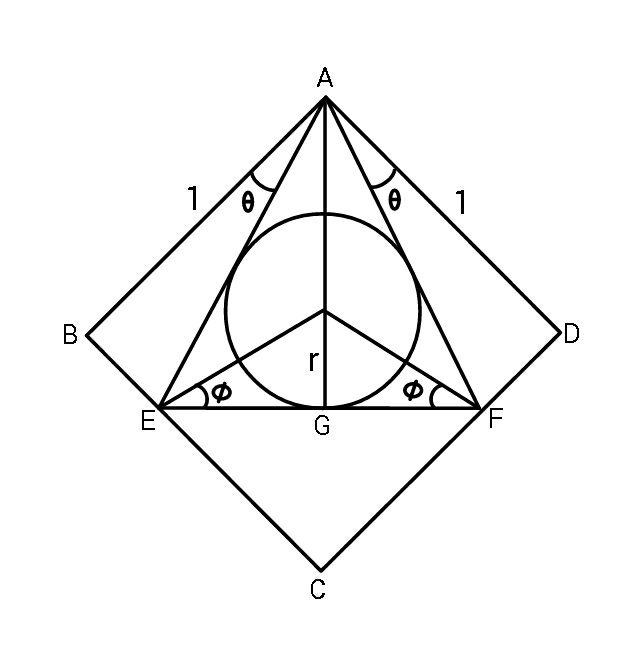
Commented by ajfour last updated on 24/Apr/20
![∠EAG=(π/4)−θ , AE=sec θ 2φ=(π/4)+θ ⇒ φ=(π/8)+(θ/2) EG=AEcos (2φ) = sec θcos ((π/4)+θ) r=EGtan φ r =(1/( (√2)))(1−tan θ)tan ((π/8)+(θ/2)) tan (π/8)=(√2)−1 let tan (θ/2)=t r=(1/( (√2)))(1−((2t)/(1−t^2 )))[((t+(√2)−1)/(1−t((√2)−1)))] say (√2)−1=a r(√2)=(((1−t^2 −2t)(t+a))/((1−t^2 )(1−at))) = ((−{t^3 +(a+2)t^2 +(2a−1)t−a})/(at^3 −t^2 −at+1)) ((d(r(√2)))/dt)=0 ⇒ (at^3 −t^2 −at+1){3t^2 +2(a+2)t+(2a−1)} +(3at^2 −2t−a){t^3 +(a+2)t^2 +(2a−1)t−a}=0 ⇒ (a+1)^2 t^4 +4a^2 t^3 −2(a^2 +1)t^2 −4t+(a−1)^2 =0 with a=(√2)−1 , appropriate t=0.08197 ⇒ θ_0 ≈9.3721° r =(1/( (√2)))(1−tan θ_0 )tan ((π/8)+(θ_0 /2)) ⇒ r_(max) ≈0.3032](https://www.tinkutara.com/question/Q90491.png)
$$\angle{EAG}=\frac{\pi}{\mathrm{4}}−\theta\:\:,\:\:{AE}=\mathrm{sec}\:\theta \\ $$$$\mathrm{2}\phi=\frac{\pi}{\mathrm{4}}+\theta\:\:\:\:\Rightarrow\:\:\phi=\frac{\pi}{\mathrm{8}}+\frac{\theta}{\mathrm{2}} \\ $$$$\:{EG}={AE}\mathrm{cos}\:\left(\mathrm{2}\phi\right) \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{sec}\:\theta\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}+\theta\right) \\ $$$$\:\:\:{r}={EG}\mathrm{tan}\:\phi \\ $$$$\:\:\:{r}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}−\mathrm{tan}\:\theta\right)\mathrm{tan}\:\left(\frac{\pi}{\mathrm{8}}+\frac{\theta}{\mathrm{2}}\right) \\ $$$$\:\:\mathrm{tan}\:\frac{\pi}{\mathrm{8}}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$${let}\:\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={t} \\ $$$$\:\:{r}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)\left[\frac{{t}+\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{1}−{t}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}\right] \\ $$$${say}\:\:\sqrt{\mathrm{2}}−\mathrm{1}={a} \\ $$$$\:\:{r}\sqrt{\mathrm{2}}=\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} −\mathrm{2}{t}\right)\left({t}+{a}\right)}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{at}\right)} \\ $$$$\:\:\:\:\:=\:\frac{−\left\{{t}^{\mathrm{3}} +\left({a}+\mathrm{2}\right){t}^{\mathrm{2}} +\left(\mathrm{2}{a}−\mathrm{1}\right){t}−{a}\right\}}{{at}^{\mathrm{3}} −{t}^{\mathrm{2}} −{at}+\mathrm{1}} \\ $$$$\frac{{d}\left({r}\sqrt{\mathrm{2}}\right)}{{dt}}=\mathrm{0} \\ $$$$\Rightarrow\:\left({at}^{\mathrm{3}} −{t}^{\mathrm{2}} −{at}+\mathrm{1}\right)\left\{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}\left({a}+\mathrm{2}\right){t}+\left(\mathrm{2}{a}−\mathrm{1}\right)\right\} \\ $$$$\:\:\:+\left(\mathrm{3}{at}^{\mathrm{2}} −\mathrm{2}{t}−{a}\right)\left\{{t}^{\mathrm{3}} +\left({a}+\mathrm{2}\right){t}^{\mathrm{2}} +\left(\mathrm{2}{a}−\mathrm{1}\right){t}−{a}\right\}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\left({a}+\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{4}} +\mathrm{4}{a}^{\mathrm{2}} {t}^{\mathrm{3}} −\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{1}\right){t}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}{t}+\left({a}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:{with}\:\:{a}=\sqrt{\mathrm{2}}−\mathrm{1}\:\:,\: \\ $$$${appropriate}\:\:{t}=\mathrm{0}.\mathrm{08197} \\ $$$$\Rightarrow\:\:\:\theta_{\mathrm{0}} \:\approx\mathrm{9}.\mathrm{3721}° \\ $$$$\:\:\:{r}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}−\mathrm{tan}\:\theta_{\mathrm{0}} \right)\mathrm{tan}\:\left(\frac{\pi}{\mathrm{8}}+\frac{\theta_{\mathrm{0}} }{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\boldsymbol{{r}}_{{max}} \approx\mathrm{0}.\mathrm{3032}\: \\ $$
Commented by Tony Lin last updated on 24/Apr/20
$${thanks}\:{sir},{I}\:{got}\:{it} \\ $$