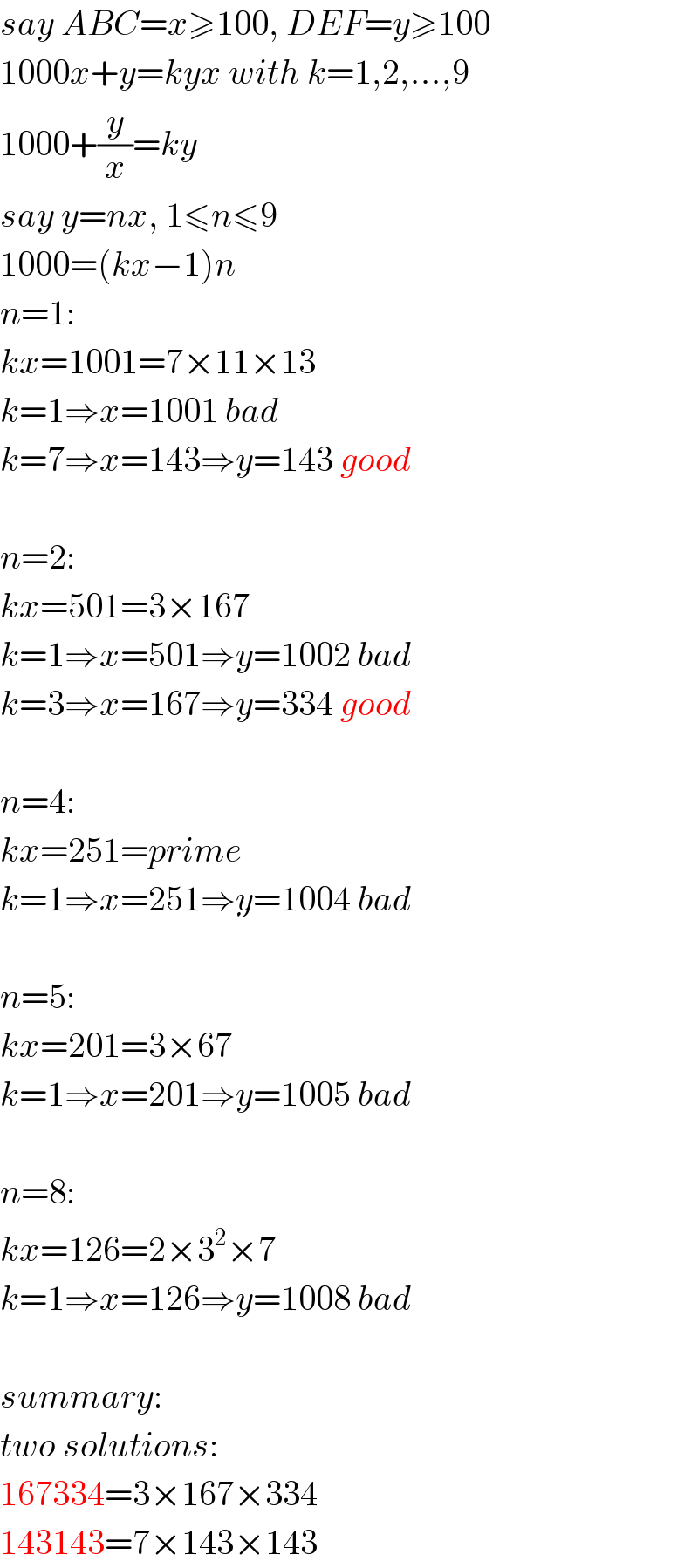ABCDEF-is-a-6-digit-number-ABC-and-DEF-are-3-digit-numbers-find-ABCDEF-satisfying-1-ABCDEF-1-ABC-DEF-2-ABCDEF-2-ABC-DEF-3-ABCDEF-3-ABC-DEF-4-ABCDEF-4-ABC-DEF-5-ABCDEF-5-ABC-DEF-6-

FacebookTweetPin

Question Number 91390 by mr W last updated on 30/Apr/20

$$ABCDEFisa6digitnumber,$$$$ABCandDEFare3digitnumbers.$$$$findABCDEFsatisfying:$$$$1)ABCDEF=1\times ABC\times DEF$$$$2)ABCDEF=2\times ABC\times DEF$$$$3)ABCDEF=3\times ABC\times DEF$$$$4)ABCDEF=4\times ABC\times DEF$$$$5)ABCDEF=5\times ABC\times DEF$$$$6)ABCDEF=6\times ABC\times DEF$$$$7)ABCDEF=7\times ABC\times DEF$$$$8)ABCDEF=8\times ABC\times DEF$$$$9)ABCDEF=9\times ABC\times DEF$$

Commented by Prithwish Sen 1 last updated on 30/Apr/20

$$\mathrm{Yes}\mathrm{Sir}\mathrm{for}\mathrm{k}=1$$$$\mathrm{Actually}\mathrm{I}\mathrm{just}\mathrm{not}\mathrm{consider}1\mathrm{as}\mathrm{the}\mathrm{divisor}\mathrm{of}$$$$1000.\mathrm{Thank}\mathrm{you}\mathrm{sir}.$$

Commented by Prithwish Sen 1 last updated on 30/Apr/20

$$\mathrm{The}\mathrm{conditions}\mathrm{are}$$$$\frac{\mathrm{DEF}}{\mathrm{ABC}}=\mathrm{k}\left(\mathbf{integer}\right)$$$$\therefore \mathbf{k}(\mathbf{n}\times \mathbf{ABC}-1)=1000(\mathrm{n}=1,2,3,\dots \dots 9)$$$$\mathbf{k}\times \mathbf{ABC}<1000$$$$\mathrm{then}\dots .$$$$\mathrm{now}\mathrm{k}=2,4\mathrm{and}8(\mathrm{any}\mathrm{higher}\mathrm{multiple}\mathrm{of}1000\mathrm{can}\mathrm{be}$$$$\mathrm{cancelled})$$$$\mathrm{now}\mathrm{for}\mathrm{k}=2$$$$\mathrm{n}\times \mathrm{ABC}=501=3\times 167$$$$\because 167\mathrm{is}\mathrm{a}\mathrm{prime}\mathrm{the}\mathrm{only}\mathrm{possibility}\mathrm{is}$$$$2(3\mathrm{\times }167-1)\mathrm{i}.\mathrm{e}.\mathrm{the}\mathrm{number}\mathrm{is}167\left(2\mathrm{\times }167\right)$$$$=167334=3\times 167\times 334$$$$\mathrm{now}\mathrm{for}\mathrm{k}=4,\mathbf{n}\times \mathbf{ABC}=251\left(\mathrm{which}\mathrm{is}\mathrm{prime}\right)$$$$\because 4\times 251>1000\mathrm{there}\mathrm{is}\mathrm{no}\mathrm{such}\mathrm{number}\mathrm{exists}.$$$$\mathrm{for}\mathrm{k}=8,\mathbf{n}\times \mathbf{ABC}=126\left(2\times 3\times 3\times 7\right)$$$$\therefore \mathrm{the}\mathrm{numbers}\mathrm{are}$$$$8(2\mathrm{\times }63-1)\Rightarrow 063504=2\times 063\times 504$$$$8(3\times 42-1)\Rightarrow 042336=3\times 042\times 336$$$$8(7\times 18-1)\Rightarrow 018144=7\times 018\times 144$$$$8(9\times 14-1)\Rightarrow 014112=9\times 014\times 112$$$$\because \mathrm{the}\mathrm{digits}\mathrm{are}\mathrm{all}\mathrm{repeated}.$$$$\mathbf{please}\mathbf{check}.$$

Commented by mr W last updated on 30/Apr/20

$$anotheroneis$$$$143143=7\times 143\times 143$$

Answered by mr W last updated on 30/Apr/20

$$sayABC=x⩾100,DEF=y⩾100$$$$1000x+y=kyxwithk=1,2,\dots ,9$$$$1000+\frac{y}{x}=ky$$$$sayy=nx,1⩽n⩽9$$$$1000=(kx-1)n$$$$n=1:$$$$kx=1001=7\times 11\times 13$$$$k=1\Rightarrow x=1001bad$$$$k=7\Rightarrow x=143\Rightarrow y=143good$$$$$$$$n=2:$$$$kx=501=3\times 167$$$$k=1\Rightarrow x=501\Rightarrow y=1002bad$$$$k=3\Rightarrow x=167\Rightarrow y=334good$$$$$$$$n=4:$$$$kx=251=prime$$$$k=1\Rightarrow x=251\Rightarrow y=1004bad$$$$$$$$n=5:$$$$kx=201=3\times 67$$$$k=1\Rightarrow x=201\Rightarrow y=1005bad$$$$$$$$n=8:$$$$kx=126=2\times 3^2\times 7$$$$k=1\Rightarrow x=126\Rightarrow y=1008bad$$$$$$$$summary:$$$$twosolutions:$$$$167334=3\times 167\times 334$$$$143143=7\times 143\times 143$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin