Question Number 147287 by mnjuly1970 last updated on 19/Jul/21
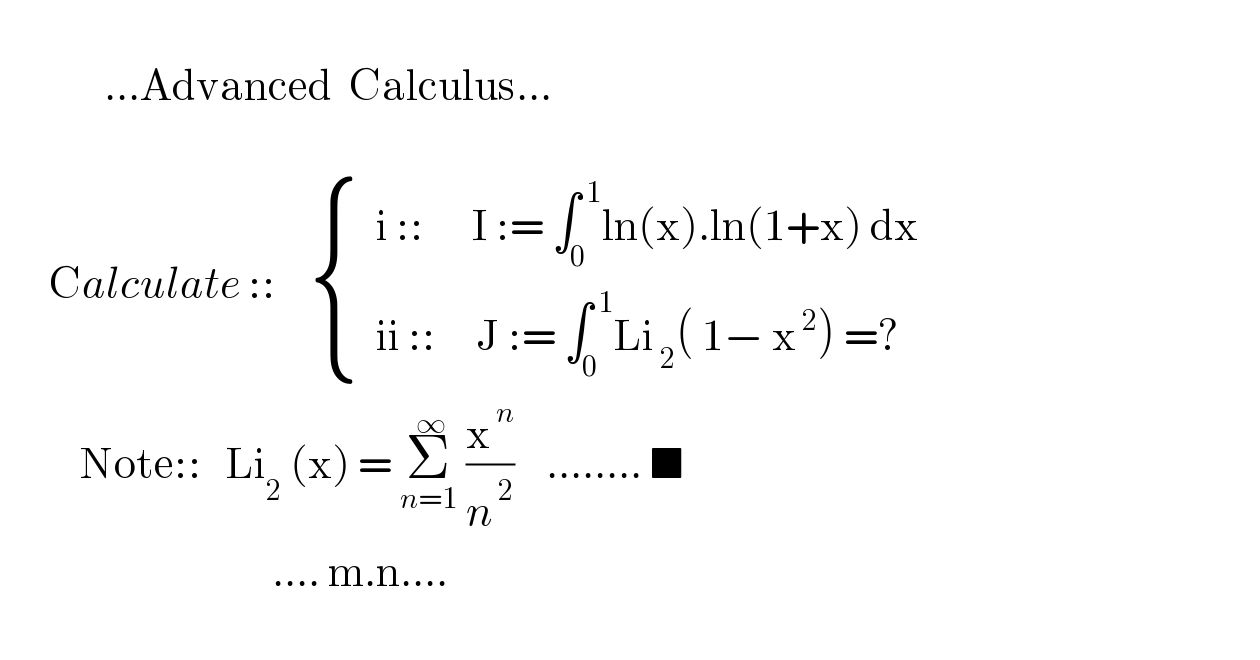
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:…\mathrm{Advanced}\:\:\mathrm{Calculus}… \\ $$$$ \\ $$$$\:\:\:\:\:\:\mathrm{C}{alculate}\:::\:\:\:\:\begin{cases}{\:\:\mathrm{i}\:::\:\:\:\:\:\:\mathrm{I}\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{ln}\left(\mathrm{x}\right).\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:\mathrm{dx}}\\{\:\:\mathrm{ii}\:::\:\:\:\:\:\mathrm{J}\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{Li}_{\:\mathrm{2}} \left(\:\mathrm{1}−\:\mathrm{x}^{\:\mathrm{2}} \right)\:=?}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{Note}::\:\:\:\mathrm{Li}_{\mathrm{2}} \:\left(\mathrm{x}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\:\infty} {\sum}}\:\frac{\mathrm{x}^{\:{n}} }{{n}^{\:\mathrm{2}} }\:\:\:\:……..\:\blacksquare\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\:\mathrm{m}.\mathrm{n}…. \\ $$$$ \\ $$
Answered by mindispower last updated on 19/Jul/21
![I=[(xln(x)−x)ln(1+x)]_0 ^1 −∫_0 ^1 ((xln(x))/(1+x))−(x/(1+x))dx =−ln(2)−∫_0 ^1 (((x+1−1)ln(x))/(1+x))−1+(1/(1+x))dx =−ln(2)−∫_0 ^1 ln(x)dx+∫_0 ^1 ((ln(x))/(1+x))dx+∫dx−∫(dx/(1+x)) =−ln(2)+1−∫_0 ^1 ((ln(1+x))/x)dx+1−ln(2) =−ln(2)−∫_0 ^1 ((ln(1−(−x)))/(−x))d(−x)+2 =ln(2)+[Li_2 (−x)]_0 ^1 =−2ln(2)+Li_2 (−1)+2=−ln(4)−(π^2 /(12))+2 J=[xli_2 (1−x^2 )]−∫_0 ^1 ((2x^2 ln(x^2 ))/(1−x^2 )) =−4∫_0 ^1 ((ln(x))/(1−x^2 ))dx+4∫_0 ^1 ln(x)dx =−2∫_0 ^1 ((ln(x))/(1−x))dx−2∫_0 ^1 ((ln(x))/(1+x))dx−4 =2Li_2 (1−x)]_0 ^1 +2∫_0 ^1 ((ln(1+x))/x)dx−4 =(π^2 /3)−2Li(−1)−4 =(π^2 /3)+(π^2 /6)−4=(π^2 /2)−4=(1/2)(π^2 −8)](https://www.tinkutara.com/question/Q147291.png)
$${I}=\left[\left({xln}\left({x}\right)−{x}\right){ln}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{xln}\left({x}\right)}{\mathrm{1}+{x}}−\frac{{x}}{\mathrm{1}+{x}}{dx} \\ $$$$=−{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({x}+\mathrm{1}−\mathrm{1}\right){ln}\left({x}\right)}{\mathrm{1}+{x}}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{x}}{dx} \\ $$$$=−{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}{dx}+\int{dx}−\int\frac{{dx}}{\mathrm{1}+{x}} \\ $$$$=−{ln}\left(\mathrm{2}\right)+\mathrm{1}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}+\mathrm{1}−{ln}\left(\mathrm{2}\right) \\ $$$$=−{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−\left(−{x}\right)\right)}{−{x}}{d}\left(−{x}\right)+\mathrm{2} \\ $$$$={ln}\left(\mathrm{2}\right)+\left[{Li}_{\mathrm{2}} \left(−{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =−\mathrm{2}{ln}\left(\mathrm{2}\right)+{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)+\mathrm{2}=−{ln}\left(\mathrm{4}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+\mathrm{2} \\ $$$${J}=\left[{xli}_{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)\right]−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}^{\mathrm{2}} {ln}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$=−\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}+\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){dx} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}−{x}}{dx}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}{dx}−\mathrm{4} \\ $$$$\left.=\mathrm{2}{Li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}−\mathrm{4} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{2}{Li}\left(−\mathrm{1}\right)−\mathrm{4} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{3}}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{4}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\mathrm{4}=\frac{\mathrm{1}}{\mathrm{2}}\left(\pi^{\mathrm{2}} −\mathrm{8}\right) \\ $$
Answered by mathmax by abdo last updated on 19/Jul/21
![Υ=∫_0 ^1 ln(x)ln(1+x)dx we have (d/dx)ln(1+x)=(1/(1+x))=Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x)=Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1))=Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) ⇒Υ=∫_0 ^1 (Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n))ln(x)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 x^n ln(x)dx U_n =∫_0 ^1 x^n ln(x)dx=[(x^(n+1) /(n+1))ln(x)]_0 ^1 −∫_0 ^1 (x^n /(n+1))dx =−(1/((n+1)^2 )) ⇒Υ=−Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(n+1)^2 ))=Σ_(n=1) ^∞ (((−1)^n )/(n(n+1)^2 )) (1/(x(x+1)^2 ))=(a/x)+(b/(x+1))+(c/((x+1)^2 ))=h(x) a=1 ,c=−1 ,lim_(x→+∞) xh(x)=0=a+b ⇒b=−1 ⇒ h(x)=(1/x)−(1/(x+1))−(1/((x+1)^2 )) ⇒Υ=Σ_(n.1) ^∞ (((−1)^n )/n)−Σ_(n=1) ^∞ (((−1)^n )/(n+1)) −Σ_(n=1) ^∞ (((−1)^n )/((n+1)^2 )) we have Σ_(n=1) ^∞ (((−1)^n )/n)=−ln2 Σ_(n=1) ^∞ (((−1)^n )/(n+1))=Σ_(n=2) ^∞ (((−1)^(n−1) )/n)=ln(2)−1 Σ_(n=1) ^∞ (((−1)^n )/((n+1)^2 ))=Σ_(n=2) ^∞ (((−1)^(n−1) )/n^2 )=−Σ_(n=2) ^∞ (((−1)^n )/n^2 ) =−(Σ_(n=1) ^∞ (((−1)^n )/n^2 )+1)=−(2^(1−2) −1)ξ(2)−1=(1/2)(π^2 /6)−1=(π^2 /(12))−1 ⇒Υ=−ln2−ln2+1−(π^2 /(12))+1 =2−2ln2−(π^2 /(12))](https://www.tinkutara.com/question/Q147300.png)
$$\Upsilon=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{dx}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{x}^{\mathrm{n}} }{\mathrm{n}} \\ $$$$\Rightarrow\Upsilon=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\right)\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}=\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\Upsilon=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{a}}{\mathrm{x}}+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{c}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{h}\left(\mathrm{x}\right) \\ $$$$\mathrm{a}=\mathrm{1}\:,\mathrm{c}=−\mathrm{1}\:\:\:,\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xh}\left(\mathrm{x}\right)=\mathrm{0}=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{h}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\Upsilon=\sum_{\mathrm{n}.\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}} \\ $$$$−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}=−\mathrm{ln2} \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }=−\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=−\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }+\mathrm{1}\right)=−\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\mathrm{1} \\ $$$$\Rightarrow\Upsilon=−\mathrm{ln2}−\mathrm{ln2}+\mathrm{1}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+\mathrm{1}\:=\mathrm{2}−\mathrm{2ln2}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
