Question Number 118886 by mnjuly1970 last updated on 20/Oct/20
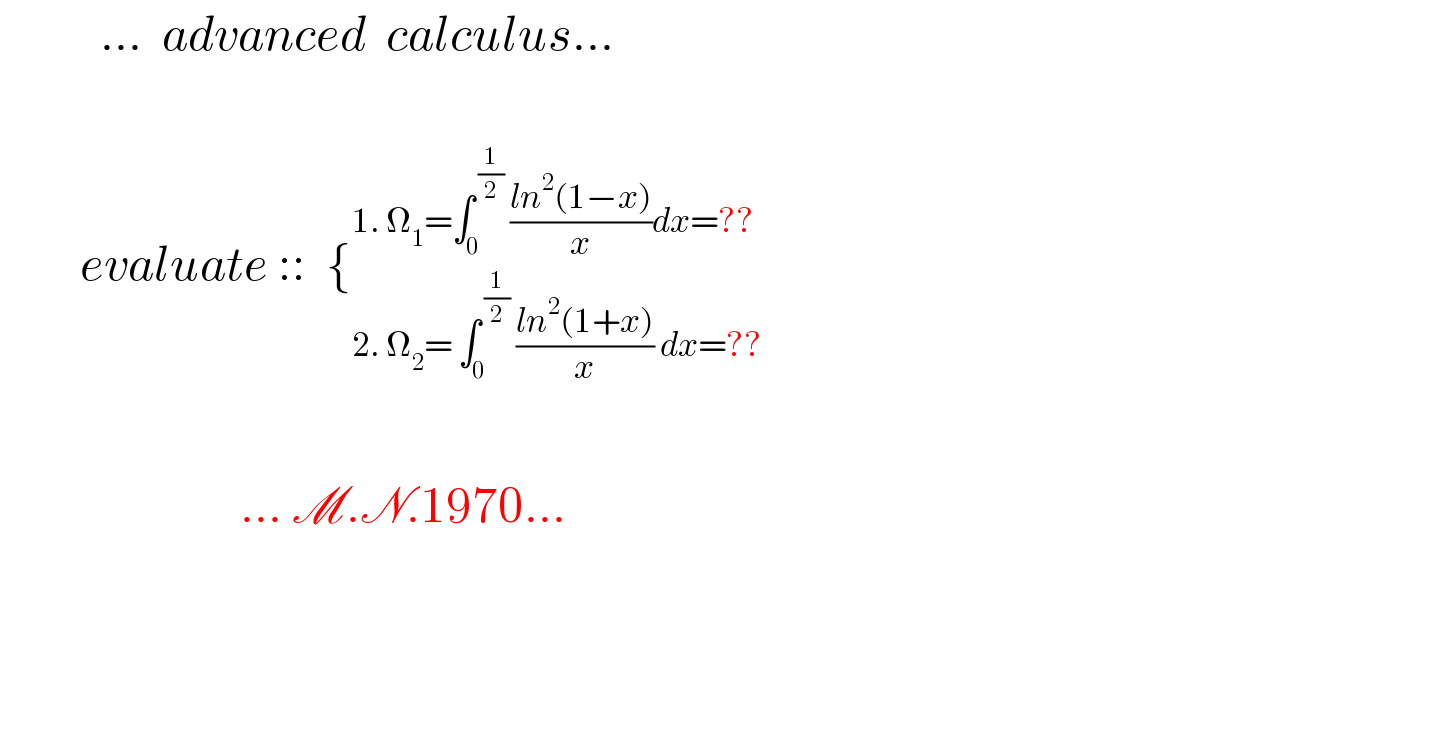
$$\:\:\:\:\:\:\:\:\:\:…\:\:{advanced}\:\:{calculus}… \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:{evaluate}\:::\:\:\left\{_{\mathrm{2}.\:\Omega_{\mathrm{2}} =\:\int_{\mathrm{0}} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{{x}}\:{dx}=??} ^{\mathrm{1}.\:\Omega_{\mathrm{1}} =\int_{\mathrm{0}} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{{x}}{dx}=??} \right. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:\mathscr{M}.\mathscr{N}.\mathrm{1970}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by mindispower last updated on 20/Oct/20
![Ω_1 =∫_0 ^(1/2) ((ln(1−x))/x)ln(1−x)dx by part withe −∫_0 ^t ((ln(1−x))/x)dx=Li_2 (t) =[−li_2 (x)ln(1−x)]_0 ^(1/2) −∫_0 ^(1/2) ((li_2 (x))/(1−x))dx =li_2 ((1/2))ln(2)−A,let 1−x=t in A Ω_1 =ln(2)li_2 ((1/2))+∫_1 ^(1/2) ((li_2 (1−t))/t)dt we have li_2 (x)+li_2 (1−x)=(π^2 /6)−ln(x)ln(1−x) ⇒Ω_1 =li_2 ((1/2))ln(2)+∫_1 ^(1/2) (π^2 /(6t))dt−∫_1 ^(1/2) ((li_2 (t))/t)dt−∫_1 ^(1/2) ((ln(t)ln(1−t))/t)dt ∫_1 ^(1/2) ((ln(t)ln(1−t))/t)dt=[((ln^2 (t)ln(1−t))/2)]_1 ^(1/2) +∫_1 ^(1/2) ((ln^2 (t))/(2(1−t)))dt 1−t=x⇒ =((ln^3 ((1/2)))/2) −∫_0 ^(1/2) ((ln^2 (1−x))/(2x)) =−((ln^3 (2))/2)−(Ω_1 /2) ⇒Ω_1 =ln(2)Li_2 ((1/2))+(π^2 /6)ln((1/2))−Li_3 ((1/2))+Li_3 (1)+((ln^3 (2))/2)+(1/2)Ω_1 li_2 ((1/2))+li_2 (1−(1/2))=(π^2 /6)−ln^2 (2)⇒li_2 ((1/2))=(π^2 /(12))−((ln^2 (2))/2) li_3 (1)=ζ(3) Ω_1 =2(ln(2)Li_2 ((1/2))−((π^2 ln(2))/6)−Li_3 ((1/2))+ζ(3)+((ln^3 (2))/2)) li_3 (z)+li_3 (1−z)+li_3 (1−(1/z))=ζ(3)+((π^2 ln(z))/6)+((ln^3 (z))/6)−((ln^2 (z))/2)ln(1−z) z=(1/2)⇒ 2li_3 ((1/2))+li_3 (−1)=ζ(3)+(π^2 /6)ln((1/2))−((ln^3 (2))/6)+((ln^3 (2))/2) Li_3 (−1)=(1/8)ζ(3)−(7/8)ζ(3)=−(3/4)ζ(3) li_3 ((1/2))=(7/8)ζ(3)−(π^2 /(12))ln(2)+((ln^3 (2))/6) Ω_1 =2(ln(2)li_2 ((1/2))−(π^2 /6)ln(2)−li_3 ((1/2))+ζ(3)+((ln^3 (2))/6)) just replqce li_2 ((1/2)),and li_3 ((1/2))... we get nswer[close[form](https://www.tinkutara.com/question/Q118940.png)
$$\Omega_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{ln}\left(\mathrm{1}−{x}\right){dx}\:{by}\:{part}\: \\ $$$${withe}\:−\int_{\mathrm{0}} ^{{t}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}={Li}_{\mathrm{2}} \left({t}\right) \\ $$$$=\left[−{li}_{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}−{x}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{li}_{\mathrm{2}} \left({x}\right)}{\mathrm{1}−{x}}{dx} \\ $$$$={li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\mathrm{2}\right)−{A},{let}\:\mathrm{1}−{x}={t}\:{in}\:{A} \\ $$$$\Omega_{\mathrm{1}} ={ln}\left(\mathrm{2}\right){li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{li}_{\mathrm{2}} \left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$${we}\:{have}\:{li}_{\mathrm{2}} \left({x}\right)+{li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right) \\ $$$$\Rightarrow\Omega_{\mathrm{1}} ={li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\mathrm{2}\right)+\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\pi^{\mathrm{2}} }{\mathrm{6}{t}}{dt}−\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{li}_{\mathrm{2}} \left({t}\right)}{{t}}{dt}−\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}\left({t}\right){ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}\left({t}\right){ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt}=\left[\frac{{ln}^{\mathrm{2}} \left({t}\right){ln}\left(\mathrm{1}−{t}\right)}{\mathrm{2}}\right]_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} +\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}^{\mathrm{2}} \left({t}\right)}{\mathrm{2}\left(\mathrm{1}−{t}\right)}{dt} \\ $$$$\mathrm{1}−{t}={x}\Rightarrow \\ $$$$=\frac{{ln}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}\:−\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{\mathrm{2}{x}}\:=−\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\Omega_{\mathrm{1}} }{\mathrm{2}}\: \\ $$$$\Rightarrow\Omega_{\mathrm{1}} ={ln}\left(\mathrm{2}\right){Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{Li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{Li}_{\mathrm{3}} \left(\mathrm{1}\right)+\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\Omega_{\mathrm{1}} \\ $$$${li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{li}_{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\Rightarrow{li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$${li}_{\mathrm{3}} \left(\mathrm{1}\right)=\zeta\left(\mathrm{3}\right) \\ $$$$\Omega_{\mathrm{1}} =\mathrm{2}\left({ln}\left(\mathrm{2}\right){Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{6}}−{Li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\zeta\left(\mathrm{3}\right)+\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{2}}\right) \\ $$$${li}_{\mathrm{3}} \left({z}\right)+{li}_{\mathrm{3}} \left(\mathrm{1}−{z}\right)+{li}_{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{{z}}\right)=\zeta\left(\mathrm{3}\right)+\frac{\pi^{\mathrm{2}} {ln}\left({z}\right)}{\mathrm{6}}+\frac{{ln}^{\mathrm{3}} \left({z}\right)}{\mathrm{6}}−\frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{2}}{ln}\left(\mathrm{1}−{z}\right) \\ $$$${z}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow \\ $$$$\mathrm{2}{li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{li}_{\mathrm{3}} \left(−\mathrm{1}\right)=\zeta\left(\mathrm{3}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{6}}+\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$${Li}_{\mathrm{3}} \left(−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)−\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)=−\frac{\mathrm{3}}{\mathrm{4}}\zeta\left(\mathrm{3}\right) \\ $$$${li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}{ln}\left(\mathrm{2}\right)+\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{6}} \\ $$$$ \\ $$$$\Omega_{\mathrm{1}} =\mathrm{2}\left({ln}\left(\mathrm{2}\right){li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left(\mathrm{2}\right)−{li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\zeta\left(\mathrm{3}\right)+\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{6}}\right) \\ $$$${just}\:{replqce}\:{li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right),{and}\:{li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)… \\ $$$${we}\:{get}\:{nswer}\left[{close}\left[{form}\right.\right. \\ $$
Commented by mnjuly1970 last updated on 21/Oct/20

$${thank}\:{you}\:{sir}… \\ $$$${very}\:{nice}… \\ $$
Commented by mindispower last updated on 21/Oct/20

$${withe}\:{pleasur} \\ $$$$ \\ $$
