Menu Close

advanced-calculus-i-prove-that-0-1-ln-1-ln-1-x-ln-1-x-dx-n-1-n-1-n-2-ii-prove-that-0-1-ln-1-x-x-1

Tinku Tara 0 Comments
Pin




Question Number 114045 by mnjuly1970 last updated on 17/Sep/20
... advanced calculus... i : prove that :: ∫_0 ^( 1) ((ln(1+ln(1−x)))/(ln(1−x))) dx =^? Σ_(n=1) ^∞ ((Γ(n+1))/n^2 ) ii: prove that :: Ω =∫_0 ^( 1) ((ln(1+x))/(x(1+x^2 )))dx =^? ((5π^2 )/(48)) m.n.july 1970#
$$\:\:\:\:\:\:\:\:…\:\:{advanced}\:{calculus}… \\ $$$$ \\ $$$${i}\::\:\:{prove}\:\:{that}\::: \\ $$$$\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{ln}\left(\mathrm{1}−{x}\right)\right)}{{ln}\left(\mathrm{1}−{x}\right)}\:{dx}\:\overset{?} {=}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\Gamma\left({n}+\mathrm{1}\right)}{{n}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${ii}:\: \\ $$$$\:\:\:\:{prove}\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\Omega\:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\:\overset{?} {=}\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{48}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{m}.{n}.{july}\:\mathrm{1970}# \\ $$$$\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 16/Sep/20
∫_0 ^1 ((log(1+x))/(x(1+x)))=∫_0 ^1 ((log(1+x))/x)−((log(1+x))/((1+x)))dx =∫_0 ^1 (−1)^n Σ_(n=1) ^∞ (x^(n−1) /n)−∫_1 ^2 ((logu)/u)du =Σ_(n=1) ^∞ (−1)^n (1/n^2 )−(1/2)[(logu)^2 ]_1 ^2 =(π^2 /(12))−(1/2)(log2)^2
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}\right)}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{x}\right)}{{x}}−\frac{{log}\left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}+{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}−\mathrm{1}} }{{n}}−\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{logu}}{{u}}{du} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\left[\left({logu}\right)^{\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{2}}\left({log}\mathrm{2}\right)^{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 16/Sep/20
I =∫_0 ^1 ((ln(1+x))/(x(1+x)))dx =∫_0 ^1 ((1/x)−(1/(x+1)))ln(1+x)dx =∫_0 ^1 ((ln(1+x))/x)dx−∫_0 ^1 ((ln(1+x))/(1+x))dx but ∫_0 ^1 ((ln(1+x))/(1+x)) dx =_(1+x=t) ∫_1 ^2 ((ln(t))/(x>t)) dt =[(1/2)ln^2 t]_1 ^2 =((ln^2 (2))/2) we have (d/dx)ln(1+x)=(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x)=Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) ⇒((ln(1+x))/x) =Σ_(n=1) ^∞ (((−1)^(n−1) x^(n−1) )/n) ⇒ ∫_0 ^1 ((ln(1+x))/x)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−{ 2^(1−2) −1}ξ(2) =(π^2 /(12)) ⇒ I =(1/2)ln^2 (2)−(π^2 /(12))
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}\mathrm{dx}\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\:\mathrm{dx}\:=_{\mathrm{1}+\mathrm{x}=\mathrm{t}} \:\:\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}>\mathrm{t}}\:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \mathrm{t}\right]_{\mathrm{1}} ^{\mathrm{2}} \:=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{dx}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }\:\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=−\left\{\:\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right\}\xi\left(\mathrm{2}\right)\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\Rightarrow\:\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 16/Sep/20
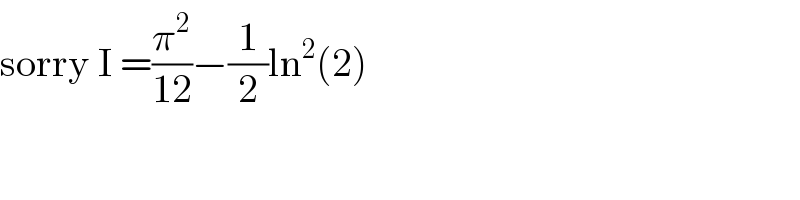
sorry I =(π^2 /(12))−(1/2)ln^2 (2)
$$\mathrm{sorry}\:\mathrm{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$
Commented by mnjuly1970 last updated on 17/Sep/20
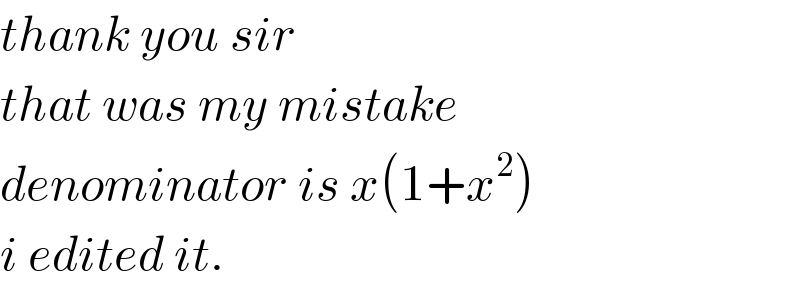
thank you sir that was my mistake denominator is x(1+x^2 ) i edited it.
$${thank}\:{you}\:{sir}\: \\ $$$${that}\:{was}\:{my}\:{mistake} \\ $$$${denominator}\:{is}\:{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$${i}\:{edited}\:{it}. \\ $$
Answered by mathmax by abdo last updated on 16/Sep/20
A =∫_0 ^1 ((ln(1+ln(1−x)))/(ln(1−x))) dx we do tbe changement ln(1−x)=−t ⇒ 1−x =e^(−t) ⇒x =1−e^(−t) ⇒ A =∫_0 ^(+∞) ((ln(1+t))/(−t)) (e^(−t) )dt =−∫_0 ^∞ ((e^(−t) ln(1+t))/t) dt =−∫_0 ^∞ e^(−t) (Σ_(n=1) ^(∞ ) (((−1)^(n−1) t^(n−1) )/n))dt =Σ_(n=1) ^(∞ ) (((−1)^n )/n) ∫_0 ^∞ t^(n−1) e^(−t) dt =Σ_(n=2) ^∞ (−1)^n ((Γ(n−1))/n) −1
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right)}{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}\:\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{changement}\:\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)=−\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{1}−\mathrm{x}\:=\mathrm{e}^{−\mathrm{t}} \:\Rightarrow\mathrm{x}\:=\mathrm{1}−\mathrm{e}^{−\mathrm{t}} \:\Rightarrow\:\mathrm{A}\:=\int_{\mathrm{0}} ^{+\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)}{−\mathrm{t}}\:\left(\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)}{\mathrm{t}}\:\mathrm{dt}\:=−\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty\:} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{t}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\right)\mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty\:} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{t}^{\mathrm{n}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\:\mathrm{dt}\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\Gamma\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{n}}\:−\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 17/Sep/20
A=−∫_0 ^( ∞) ((ln(1−t)e^(−t) )/t)dt is correct.please check it .thank you so much for your effort .
$${A}=−\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left(\mathrm{1}−{t}\right){e}^{−{t}} }{{t}}{dt}\:\:{is}\: \\ $$$${correct}.{please}\:{check}\:{it} \\ $$$$.{thank}\:{you}\:{so}\:{much}\:{for} \\ $$$${your}\:{effort}\:. \\ $$
Answered by mindispower last updated on 17/Sep/20
i) ∫_0 ^1 ((ln(1+ln(1−x)))/(ln(1−x)))dx=∫_0 ^1 ((ln(1+ln(x)))/(ln(x)))dx =∫_0 ^∞ ((ln(1−x))/(−x))e^(−x) dx somthing wrong ln(1−x)∈C x>1
$$\left.{i}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{ln}\left(\mathrm{1}−{x}\right)\right)}{{ln}\left(\mathrm{1}−{x}\right)}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{ln}\left({x}\right)\right)}{{ln}\left({x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{1}−{x}\right)}{−{x}}{e}^{−{x}} {dx}\:{somthing}\:{wrong} \\ $$$${ln}\left(\mathrm{1}−{x}\right)\in\mathbb{C}\:\:{x}>\mathrm{1} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *