Menu Close

advanced-calculus-prove-that-n-1-H-n-n-4-3-5-2-3-where-H-n-1-1-2-1-3-1-n-

Tinku Tara 0 Comments
Pin




Question Number 126726 by mnjuly1970 last updated on 23/Dec/20
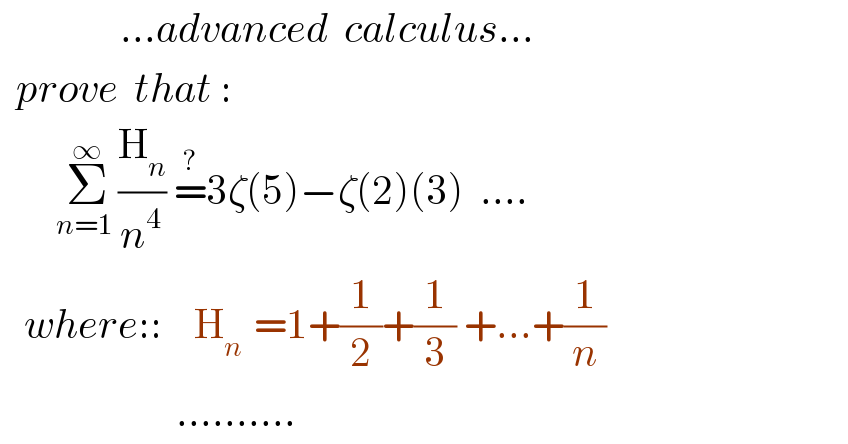
...advanced calculus... prove that : Σ_(n=1 ) ^∞ (H_n /n^4 ) =^? 3ζ(5)−ζ(2)(3) .... where:: H_(n ) =1+(1/2)+(1/3) +...+(1/n) ..........
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{advanced}\:\:{calculus}… \\ $$$$\:\:{prove}\:\:{that}\::\: \\ $$$$\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\frac{\mathrm{H}_{{n}} }{{n}^{\mathrm{4}} }\:\overset{?} {=}\mathrm{3}\zeta\left(\mathrm{5}\right)−\zeta\left(\mathrm{2}\right)\left(\mathrm{3}\right)\:\:…. \\ $$$$\:\:\:{where}::\:\:\:\:\mathrm{H}_{{n}\:} \:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\:+…+\frac{\mathrm{1}}{{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………. \\ $$
Answered by mindispower last updated on 24/Dec/20
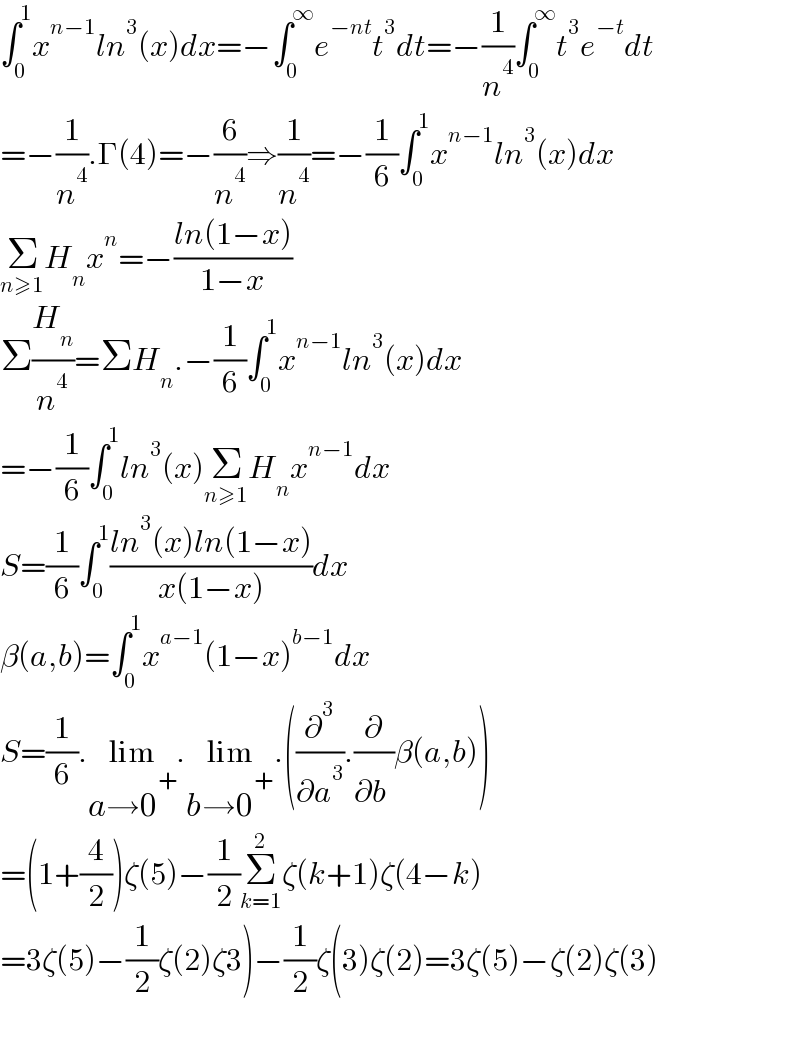
∫_0 ^1 x^(n−1) ln^3 (x)dx=−∫_0 ^∞ e^(−nt) t^3 dt=−(1/n^4 )∫_0 ^∞ t^3 e^(−t) dt =−(1/n^4 ).Γ(4)=−(6/n^4 )⇒(1/n^4 )=−(1/6)∫_0 ^1 x^(n−1) ln^3 (x)dx Σ_(n≥1) H_n x^n =−((ln(1−x))/(1−x)) Σ(H_n /n^4 )=ΣH_n .−(1/6)∫_0 ^1 x^(n−1) ln^3 (x)dx =−(1/6)∫_0 ^1 ln^3 (x)Σ_(n≥1) H_n x^(n−1) dx S=(1/6)∫_0 ^1 ((ln^3 (x)ln(1−x))/(x(1−x)))dx β(a,b)=∫_0 ^1 x^(a−1) (1−x)^(b−1) dx S=(1/6).lim_(a→0^+ ) .lim_(b→0^+ ) .((∂^3 /∂a^3 ).(∂/∂b^ )β(a,b)) =(1+(4/2))ζ(5)−(1/2)Σ_(k=1) ^2 ζ(k+1)ζ(4−k) =3ζ(5)−(1/2)ζ(2)ζ3)−(1/2)ζ(3)ζ(2)=3ζ(5)−ζ(2)ζ(3)
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}^{\mathrm{3}} \left({x}\right){dx}=−\int_{\mathrm{0}} ^{\infty} {e}^{−{nt}} {t}^{\mathrm{3}} {dt}=−\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{3}} {e}^{−{t}} {dt} \\ $$$$=−\frac{\mathrm{1}}{{n}^{\mathrm{4}} }.\Gamma\left(\mathrm{4}\right)=−\frac{\mathrm{6}}{{n}^{\mathrm{4}} }\Rightarrow\frac{\mathrm{1}}{{n}^{\mathrm{4}} }=−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}^{\mathrm{3}} \left({x}\right){dx} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}{H}_{{n}} {x}^{{n}} =−\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}−{x}} \\ $$$$\Sigma\frac{{H}_{{n}} }{{n}^{\mathrm{4}} }=\Sigma{H}_{{n}} .−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}^{\mathrm{3}} \left({x}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}^{\mathrm{3}} \left({x}\right)\underset{{n}\geqslant\mathrm{1}} {\sum}{H}_{{n}} {x}^{{n}−\mathrm{1}} {dx} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{3}} \left({x}\right){ln}\left(\mathrm{1}−{x}\right)}{{x}\left(\mathrm{1}−{x}\right)}{dx} \\ $$$$\beta\left({a},{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{b}−\mathrm{1}} {dx} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{6}}.\underset{{a}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}.\underset{{b}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}.\left(\frac{\partial^{\mathrm{3}} }{\partial{a}^{\mathrm{3}} }.\frac{\partial}{\partial{b}^{} }\beta\left({a},{b}\right)\right) \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{2}}\right)\zeta\left(\mathrm{5}\right)−\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\zeta\left({k}+\mathrm{1}\right)\zeta\left(\mathrm{4}−{k}\right) \\ $$$$\left.=\mathrm{3}\zeta\left(\mathrm{5}\right)−\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right)\zeta\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{3}\right)\zeta\left(\mathrm{2}\right)=\mathrm{3}\zeta\left(\mathrm{5}\right)−\zeta\left(\mathrm{2}\right)\zeta\left(\mathrm{3}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 24/Dec/20
very nice as always sir minds...
$${very}\:{nice}\:{as}\:{always}\:{sir}\:{minds}… \\ $$
Commented by mindispower last updated on 25/Dec/20
always pleasur
$${always}\:{pleasur} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *