Question Number 117574 by mnjuly1970 last updated on 12/Oct/20
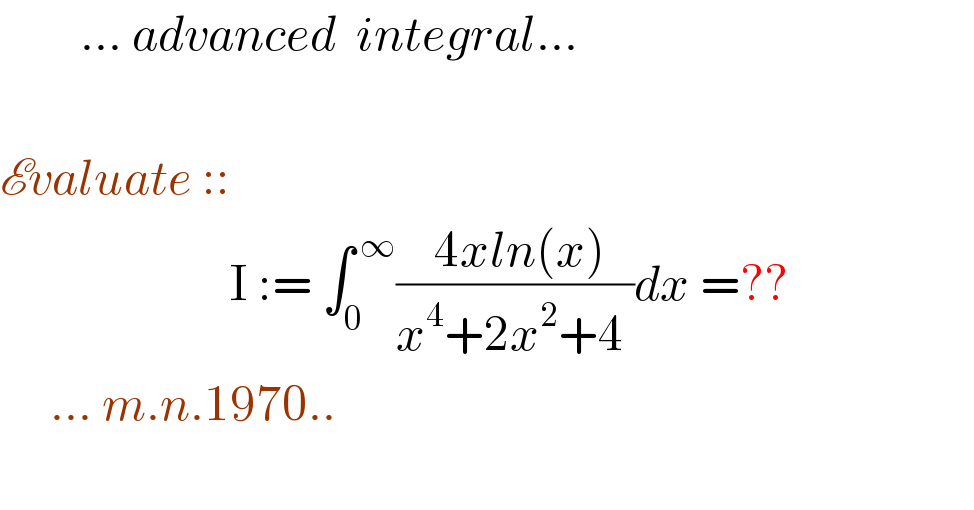
$$\:\:\:\:\:\:\:\:…\:{advanced}\:\:{integral}… \\ $$$$\:\:\:\:\:\: \\ $$$$\mathscr{E}{valuate}\:::\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}\::=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:\mathrm{4}{xln}\left({x}\right)}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}\:}{dx}\:=??\: \\ $$$$\:\:\:\:\:…\:{m}.{n}.\mathrm{1970}.. \\ $$$$\: \\ $$
Answered by mindispower last updated on 12/Oct/20
![x^2 =t⇒ I=∫_0 ^∞ ((ln(t))/(t^2 +2t+4)) t⇒2s⇒∫_0 ^∞ ((ln(2s).2ds)/(4(s^2 +s+1)))=∫_0 ^∞ ((ln(2)ds)/(2(s^2 +s+1)=I))+(1/2)∫_0 ^∞ ((ln(x))/(x^2 +x+1=J)) firstI basic J =(1/2)∫_0 ^1 ((ln(x))/(x^2 +x+1))dx+(1/2)∫_1 ^∞ ((ln(x))/(x^2 +x+1))dx x=(1/t) in 2nd ⇒dx=((−dt)/t^2 ) =(1/2)∫_1 ^0 ((ln(t))/(1+t+t^2 ))=−(1/2)∫_0 ^1 ((ln(x))/(1+x+x^2 )) ⇒we have juste tofind ∫_0 ^∞ ((ln(2)dx)/(x^2 +x+1)).(1/2)=((ln(2))/2)∫_0 ^∞ (dx/((x+(1/2))^2 +(3/4))) =((2ln(2))/3)∫_0 ^∞ (dx/((((2x)/( (√3)))+(1/( (√3))))))=((ln(2))/( (√3)))[arctan(((2x)/( (√3)))+(1/( (√3))))]_0 ^∞ =((ln(2))/( (√3)))[(π/2)−(π/6)]=((πln(2))/( 3(√3)))](https://www.tinkutara.com/question/Q117590.png)
$${x}^{\mathrm{2}} ={t}\Rightarrow \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{4}} \\ $$$${t}\Rightarrow\mathrm{2}{s}\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{2}{s}\right).\mathrm{2}{ds}}{\mathrm{4}\left({s}^{\mathrm{2}} +{s}+\mathrm{1}\right)}=\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{2}\right){ds}}{\mathrm{2}\left({s}^{\mathrm{2}} +{s}+\mathrm{1}\right)={I}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} +{x}+\mathrm{1}={J}} \\ $$$${firstI}\:{basic} \\ $$$${J}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$${x}=\frac{\mathrm{1}}{{t}}\:{in}\:\mathrm{2}{nd}\:\Rightarrow{dx}=\frac{−{dt}}{{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{0}} \frac{{ln}\left({t}\right)}{\mathrm{1}+{t}+{t}^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{we}\:{have}\:{juste}\:{tofind} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{2}\right){dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}.\frac{\mathrm{1}}{\mathrm{2}}=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left(\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)}=\frac{{ln}\left(\mathrm{2}\right)}{\:\sqrt{\mathrm{3}}}\left[{arctan}\left(\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\:\sqrt{\mathrm{3}}}\left[\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{6}}\right]=\frac{\pi{ln}\left(\mathrm{2}\right)}{\:\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 12/Oct/20
$${tayeballah}\:\:{thank}\:{you}\:{so} \\ $$$${much}… \\ $$
Commented by mindispower last updated on 14/Oct/20

$${withe}?{pleasur}\: \\ $$
