Question Number 130889 by mnjuly1970 last updated on 30/Jan/21
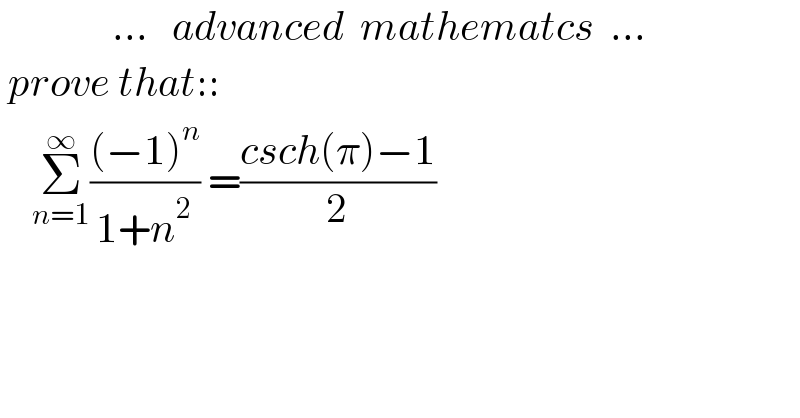
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:\:\:{advanced}\:\:{mathematcs}\:\:… \\ $$$$\:{prove}\:{that}:: \\ $$$$\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{1}+{n}^{\mathrm{2}} }\:=\frac{{csch}\left(\pi\right)−\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by mindispower last updated on 30/Jan/21
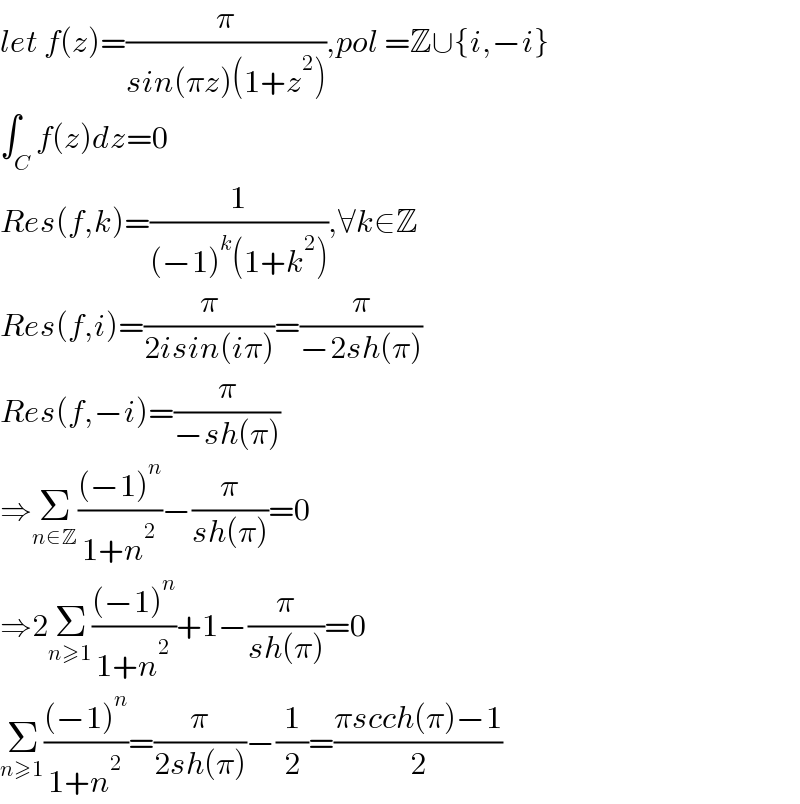
$${let}\:{f}\left({z}\right)=\frac{\pi}{{sin}\left(\pi{z}\right)\left(\mathrm{1}+{z}^{\mathrm{2}} \right)},{pol}\:=\mathbb{Z}\cup\left\{{i},−{i}\right\} \\ $$$$\int_{{C}} {f}\left({z}\right){dz}=\mathrm{0} \\ $$$${Res}\left({f},{k}\right)=\frac{\mathrm{1}}{\left(−\mathrm{1}\right)^{{k}} \left(\mathrm{1}+{k}^{\mathrm{2}} \right)},\forall{k}\in\mathbb{Z} \\ $$$${Res}\left({f},{i}\right)=\frac{\pi}{\mathrm{2}{isin}\left({i}\pi\right)}=\frac{\pi}{−\mathrm{2}{sh}\left(\pi\right)} \\ $$$${Res}\left({f},−{i}\right)=\frac{\pi}{−{sh}\left(\pi\right)} \\ $$$$\Rightarrow\underset{{n}\in\mathbb{Z}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{1}+{n}^{\mathrm{2}} }−\frac{\pi}{{sh}\left(\pi\right)}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{1}+{n}^{\mathrm{2}} }+\mathrm{1}−\frac{\pi}{{sh}\left(\pi\right)}=\mathrm{0} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{1}+{n}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}{sh}\left(\pi\right)}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\pi{scch}\left(\pi\right)−\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 30/Jan/21
$${tayeballah}\:{mr}\:{power}.. \\ $$$${thank}\:{you}… \\ $$
Commented by mindispower last updated on 30/Jan/21
$${withe}\:{pleasur}\:{god}\:{bless}\:{you} \\ $$
