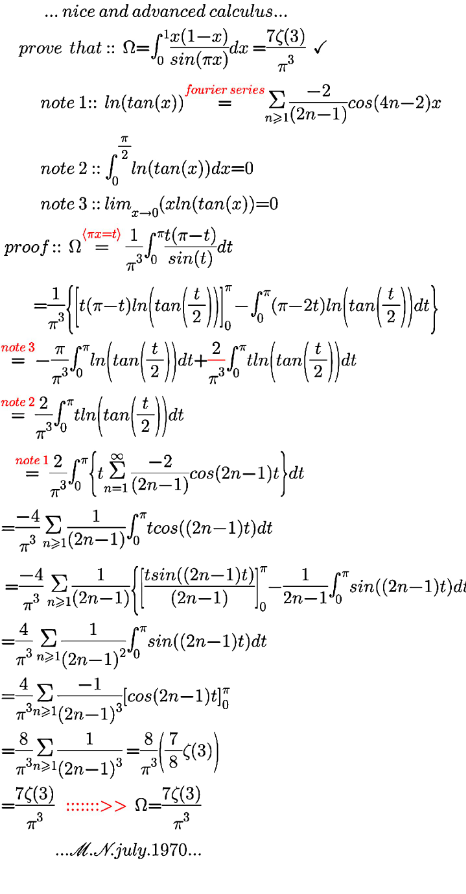Question Number 121282 by mnjuly1970 last updated on 06/Nov/20
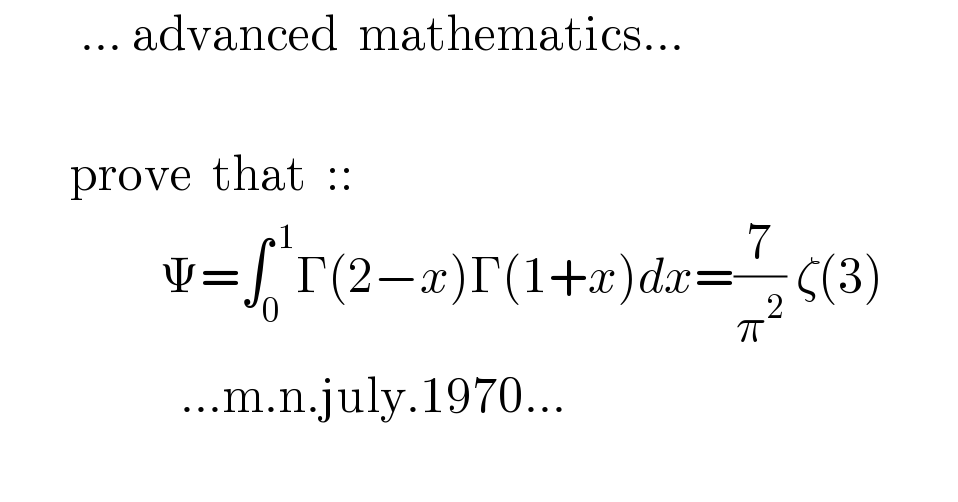
$$\:\:\:\:\:\:\:\:…\:\mathrm{advanced}\:\:\mathrm{mathematics}… \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{prove}\:\:\mathrm{that}\:\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Psi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \Gamma\left(\mathrm{2}−{x}\right)\Gamma\left(\mathrm{1}+{x}\right){dx}=\frac{\mathrm{7}}{\pi^{\mathrm{2}} }\:\zeta\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\mathrm{m}.\mathrm{n}.\mathrm{july}.\mathrm{1970}… \\ $$$$ \\ $$
Answered by mindispower last updated on 06/Nov/20
![Ψ=∫_0 ^1 (1−x)(−x)Γ(−x)Γ(1+x)dx Γ(−x)Γ(1+x)=(π/(sin(−πx)))=−(π/(sin(πx))) Ψ=π∫_0 ^1 ((x(x−1))/(sin(πx)))dx,We use integration By part ⇒Ψ=(1/2)[ln(((1−cos(πx))/(1+cos(πx))))x(x−1)]_0 ^1 −(1/2)∫(2x−1)ln(((1−cos(πx))/(1+cos(πx))))dx Ψ=−(1/2)∫_0 ^1 (2x−1)ln(((2sin^2 (((πx)/2)))/(2cos^2 (((πx)/2)))))dx =−∫_0 ^1 (2x−1)ln(tg(((πx)/2)))dx let z=((πx)/2)⇒dx=(2/π)dz =−(2/π)∫_0 ^(π/2) (((4z)/π)−1)ln(tg(z)).dz =−(8/π^2 )∫_0 ^(π/2) zln(tg(z))dz ∀x∈[0,(π/2)[ we have ln(tg(x))=−2Σ((cos(2(2n−1)x))/(2n−1)) Ψ=−(8/π^2 )Σ_(n≥1) ((−2)/((2n−1))) ∫xcos(2(2n−1)x)dx IBP −(8/π^2 ).2Σ_(n≥1) ∫_0 ^(π/2) (1/(2(2n−1)^2 ))sin(2(2n−1)) =−((16)/π^2 )Σ_(n≥1) [((cos((2n−1)π)−1)/(4(2n−1)^3 ))] =.−((16)/π^2 ).Σ_(n≥1) −(1/(2(2n−1)^3 ))=−((16)/π^2 ).−(1/2)((7/8)ζ(3)) =(7/π^2 )ζ(3)](https://www.tinkutara.com/question/Q121335.png)
$$\Psi=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)\left(−{x}\right)\Gamma\left(−{x}\right)\Gamma\left(\mathrm{1}+{x}\right){dx} \\ $$$$\Gamma\left(−{x}\right)\Gamma\left(\mathrm{1}+{x}\right)=\frac{\pi}{{sin}\left(−\pi{x}\right)}=−\frac{\pi}{{sin}\left(\pi{x}\right)} \\ $$$$\Psi=\pi\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}\left({x}−\mathrm{1}\right)}{{sin}\left(\pi{x}\right)}{dx},{We}\:{use}\:{integration}\:{By}\:{part} \\ $$$$\Rightarrow\Psi=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left(\frac{\mathrm{1}−{cos}\left(\pi{x}\right)}{\mathrm{1}+{cos}\left(\pi{x}\right)}\right){x}\left({x}−\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{2}{x}−\mathrm{1}\right){ln}\left(\frac{\mathrm{1}−{cos}\left(\pi{x}\right)}{\mathrm{1}+{cos}\left(\pi{x}\right)}\right){dx} \\ $$$$\Psi=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right){ln}\left(\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi{x}}{\mathrm{2}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\pi{x}}{\mathrm{2}}\right)}\right){dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right){ln}\left({tg}\left(\frac{\pi{x}}{\mathrm{2}}\right)\right){dx} \\ $$$${let}\:{z}=\frac{\pi{x}}{\mathrm{2}}\Rightarrow{dx}=\frac{\mathrm{2}}{\pi}{dz} \\ $$$$=−\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{4}{z}}{\pi}−\mathrm{1}\right){ln}\left({tg}\left({z}\right)\right).{dz} \\ $$$$=−\frac{\mathrm{8}}{\pi^{\mathrm{2}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {zln}\left({tg}\left({z}\right)\right){dz} \\ $$$$\forall{x}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\left[\:{we}\:{have}\right.\right. \\ $$$${ln}\left({tg}\left({x}\right)\right)=−\mathrm{2}\Sigma\frac{{cos}\left(\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right){x}\right)}{\mathrm{2}{n}−\mathrm{1}} \\ $$$$\Psi=−\frac{\mathrm{8}}{\pi^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{−\mathrm{2}}{\left(\mathrm{2}{n}−\mathrm{1}\right)}\:\int{xcos}\left(\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right){x}\right){dx}\:{IBP} \\ $$$$−\frac{\mathrm{8}}{\pi^{\mathrm{2}} }.\mathrm{2}\underset{{n}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }{sin}\left(\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)\right) \\ $$$$=−\frac{\mathrm{16}}{\pi^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\sum}\left[\frac{{cos}\left(\left(\mathrm{2}{n}−\mathrm{1}\right)\pi\right)−\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{3}} }\right] \\ $$$$=.−\frac{\mathrm{16}}{\pi^{\mathrm{2}} }.\underset{{n}\geqslant\mathrm{1}} {\sum}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{3}} }=−\frac{\mathrm{16}}{\pi^{\mathrm{2}} }.−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)\right) \\ $$$$=\frac{\mathrm{7}}{\pi^{\mathrm{2}} }\zeta\left(\mathrm{3}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 06/Nov/20
$${bravo}\:\:{sir}\:{mindspower} \\ $$$${good}\:{for}\:{you}… \\ $$
Commented by mnjuly1970 last updated on 06/Nov/20