Question Number 127725 by mnjuly1970 last updated on 01/Jan/21
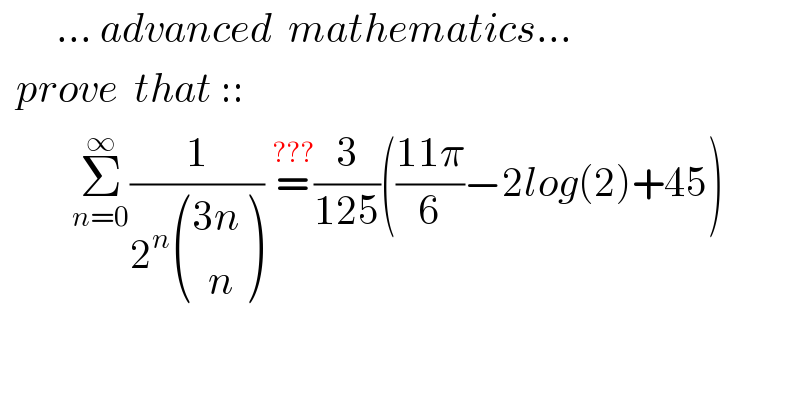
$$\:\:\:\:\:\:\:…\:{advanced}\:\:{mathematics}… \\ $$$$\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} \begin{pmatrix}{\mathrm{3}{n}}\\{\:\:{n}}\end{pmatrix}}\:\overset{???} {=}\frac{\mathrm{3}}{\mathrm{125}}\left(\frac{\mathrm{11}\pi}{\mathrm{6}}−\mathrm{2}{log}\left(\mathrm{2}\right)+\mathrm{45}\right) \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 01/Jan/21
![1+((2!)/(2∙3!))+((4!2!)/(2^2 ∙6!))+((6!3!)/(2^3 9!))+∙∙∙(((2n)!n!)/(2^n (3n)!))+∙∙∙ S_n =Σ_(n=0) ^∞ ((Γ(2n+1)Γ(n+1))/(2^n Γ(3n+1)))=Σ_(n=0) ^∞ ((nΓ(2n+1)Γ(n))/(2^n Γ(3n+1))) =Σ_(n=0) ^∞ (n/2^n )β(2n+1, n)=Σ_(n=0) ^∞ (n/2^n )∫_0 ^1 x^(2n) (1−x)^(n−1) dx =∫_0 ^1 {Σ_(n=0) ^∞ [(n/2^n )x^(2n) (1−x)^(n−1) ]}dx=∫_0 ^1 {(1/(1−x))∙Σ_(n=0) ^∞ n(((x^2 (1−x))/2))^n }dx S(t)=Σ_(k=0) ^∞ t^k =(1/(1−t)) ⇒S′(t)=Σ_(k=0) ^∞ kt^(k−1) =(1/((1−t)^2 )) tS′(t)=Σ_(k=0) ^∞ kt^k =(t/((1−t)^2 )) Σ_(n=0) ^∞ n(((x^2 (1−x))/2))^n =(((x^2 (1−x))/2)/((1−((x^2 (1−x))/2))^2 ))=((x^2 (1−x))/2)∙(4/((2−x^2 +x^3 )^2 )) =((2x^2 (1−x))/((x^3 −x^2 +2)^2 )) S_n =∫_0 ^1 {(1/(1−x))∙((2x^2 (1−x))/((x^3 −x^2 +2)^2 ))}dx=∫_0 ^1 ((2x^2 dx)/((x^3 −x^2 +2)^2 )) =∫_0 ^1 ((2x^2 )/(((x+1)(x^2 −2x+2))^2 )) f(x)=2((x/((x+1)(x^2 −2x+2))))^2 =(2/(25))(((x+2)/(x^2 −2x+2))−(1/(x+1)))^2 =(2/(25))(((x^2 +4x+4)/((x^2 −2x+2)^2 ))−((2(x+2))/((x+1)(x^2 −2x+2)))+(1/((x+1)^2 ))) =(2/(25))((1/(x^2 −2x+2))+((6x+2)/((x^2 −2x+2)^2 ))−(2/(5(x+1)))+((2(x−1))/(x^2 −2x+2))+(1/((x+1)^2 ))) 6x+2=3(2x−2)+8 ∫_0 ^1 f(x)dx=(2/(25))[tan^(−1) (x−1)−(3/(x^2 −2x+2))+8∫(dx/(((x−1)^2 +1)^2 )) [−((2ln(x+1))/5)−ln(x^2 −2x+2)−(1/(x+1))]_0 ^1 S_n =(2/(25))(−3−((2ln2)/5)−(1/2))−(2/(25))(−(π/4)−(3/2)−ln2−1)−((2π)/(25)) =−(2/(25))+((6ln2)/(125))−((6π)/(100)) Typos](https://www.tinkutara.com/question/Q127727.png)
$$\mathrm{1}+\frac{\mathrm{2}!}{\mathrm{2}\centerdot\mathrm{3}!}+\frac{\mathrm{4}!\mathrm{2}!}{\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{6}!}+\frac{\mathrm{6}!\mathrm{3}!}{\mathrm{2}^{\mathrm{3}} \mathrm{9}!}+\centerdot\centerdot\centerdot\frac{\left(\mathrm{2n}\right)!\mathrm{n}!}{\mathrm{2}^{\mathrm{n}} \left(\mathrm{3n}\right)!}+\centerdot\centerdot\centerdot \\ $$$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma\left(\mathrm{2n}+\mathrm{1}\right)\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}^{\mathrm{n}} \Gamma\left(\mathrm{3n}+\mathrm{1}\right)}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{n}\Gamma\left(\mathrm{2n}+\mathrm{1}\right)\Gamma\left(\mathrm{n}\right)}{\mathrm{2}^{\mathrm{n}} \Gamma\left(\mathrm{3n}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }\beta\left(\mathrm{2n}+\mathrm{1},\:\mathrm{n}\right)=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{2n}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{dx} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }\mathrm{x}^{\mathrm{2n}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \right]\right\}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\centerdot\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{n}\left(\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{2}}\right)^{\mathrm{n}} \right\}\mathrm{dx} \\ $$$$\mathrm{S}\left(\mathrm{t}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{t}^{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow\mathrm{S}'\left(\mathrm{t}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{kt}^{\mathrm{k}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} } \\ $$$$\mathrm{tS}'\left(\mathrm{t}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{kt}^{\mathrm{k}} =\frac{\mathrm{t}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} } \\ $$$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{n}\left(\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{2}}\right)^{\mathrm{n}} =\frac{\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{2}}}{\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{2}}\centerdot\frac{\mathrm{4}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\mathrm{S}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\centerdot\frac{\mathrm{2x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\right\}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2x}^{\mathrm{2}} \mathrm{dx}}{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2x}^{\mathrm{2}} }{\left(\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}\right)\right)^{\mathrm{2}} } \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2}\left(\frac{\mathrm{x}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}\right)}\right)^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{25}}\left(\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{25}}\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{4}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{25}}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}}+\frac{\mathrm{6x}+\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{5}\left(\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}}+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\mathrm{6x}+\mathrm{2}=\mathrm{3}\left(\mathrm{2x}−\mathrm{2}\right)+\mathrm{8} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{25}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}−\mathrm{1}\right)−\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}}+\mathrm{8}\int\frac{\mathrm{dx}}{\left(\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[−\frac{\mathrm{2ln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{5}}−\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{2}}{\mathrm{25}}\left(−\mathrm{3}−\frac{\mathrm{2ln2}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{2}}{\mathrm{25}}\left(−\frac{\pi}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{ln2}−\mathrm{1}\right)−\frac{\mathrm{2}\pi}{\mathrm{25}} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{2}}{\mathrm{25}}+\frac{\mathrm{6ln2}}{\mathrm{125}}−\frac{\mathrm{6}\pi}{\mathrm{100}}\: \\ $$$${Typos} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jan/21
![Σ_(n=0) ^∞ (1/(2^n (((2n)),(n) )))=Σ_(n=0) ^∞ ((Γ^2 (n+1))/(2^n Γ(2n+1)))=∫_0 ^1 Σ_(n=0) ^∞ (n/2^n )x^n (1−x)^(n−1) dx =2∫_0 ^1 (x/((2−x(1−x))^2 ))dx=∫_0 ^1 ((2x−1)/((x^2 −x+2)^2 ))+∫_0 ^1 (1/((x^2 −x+2)^2 ))dx =∫_0 ^1 (1/(((x−((1+i(√7))/2))(x−((1−i(√7))/2)))^2 ))dx=−(1/7)∫_0 ^1 (1/((x−((1+i(√7))/2))^2 ))+(1/((x−((1−i(√7))/2))^2 ))−(2/((x^2 −x+2))) =(1/7)∫_0 ^1 (1/(x^2 −x+2))dx+(1/7)[.((2x−1)/(x^2 −x+2))]_0 ^1 =(8/(7(√7)))tan^(−1) (1/( (√7)))+(1/7)](https://www.tinkutara.com/question/Q127728.png)
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} \begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma^{\mathrm{2}} \left({n}+\mathrm{1}\right)}{\mathrm{2}^{{n}} \Gamma\left(\mathrm{2}{n}+\mathrm{1}\right)}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}}{\mathrm{2}^{{n}} }{x}^{{n}} \left(\mathrm{1}−{x}\right)^{{n}−\mathrm{1}} {dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\left(\mathrm{2}−{x}\left(\mathrm{1}−{x}\right)\right)^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)^{\mathrm{2}} }+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\left({x}−\frac{\mathrm{1}+{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\right)\left({x}−\frac{\mathrm{1}−{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }{dx}=−\frac{\mathrm{1}}{\mathrm{7}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}+{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}−{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}{dx}+\frac{\mathrm{1}}{\mathrm{7}}\left[.\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{8}}{\mathrm{7}\sqrt{\mathrm{7}}}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{7}}}+\frac{\mathrm{1}}{\mathrm{7}} \\ $$
Commented by mnjuly1970 last updated on 01/Jan/21

$${nice}\:{vety}\:{nicr} \\ $$
