Question Number 125169 by TANMAY PANACEA last updated on 08/Dec/20

$${algebra} \\ $$
Commented by TANMAY PANACEA last updated on 08/Dec/20

$$ \\ $$
Commented by TANMAY PANACEA last updated on 08/Dec/20

Commented by kaivan.ahmadi last updated on 08/Dec/20
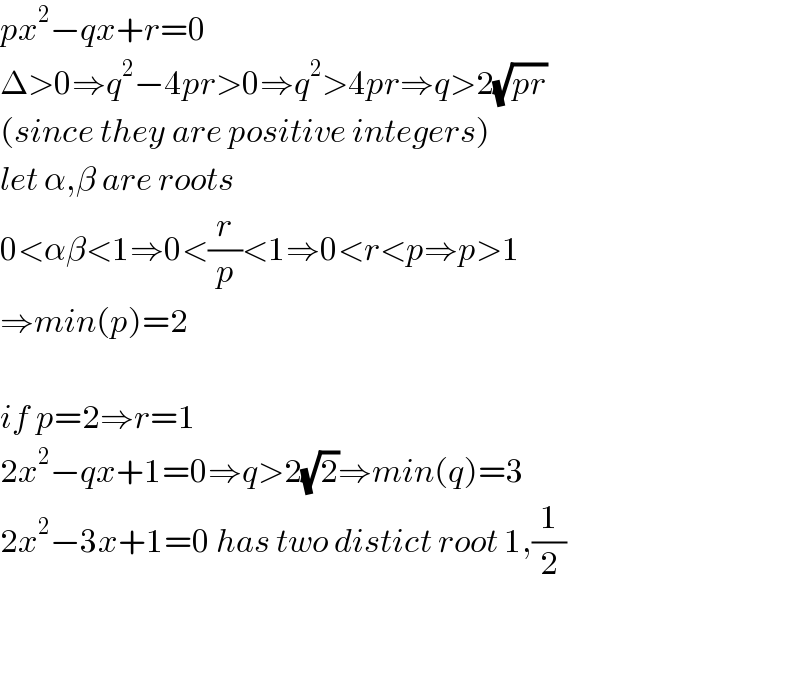
$${px}^{\mathrm{2}} −{qx}+{r}=\mathrm{0} \\ $$$$\Delta>\mathrm{0}\Rightarrow{q}^{\mathrm{2}} −\mathrm{4}{pr}>\mathrm{0}\Rightarrow{q}^{\mathrm{2}} >\mathrm{4}{pr}\Rightarrow{q}>\mathrm{2}\sqrt{{pr}} \\ $$$$\left({since}\:{they}\:{are}\:{positive}\:{integers}\right) \\ $$$${let}\:\alpha,\beta\:{are}\:{roots} \\ $$$$\mathrm{0}<\alpha\beta<\mathrm{1}\Rightarrow\mathrm{0}<\frac{{r}}{{p}}<\mathrm{1}\Rightarrow\mathrm{0}<{r}<{p}\Rightarrow{p}>\mathrm{1} \\ $$$$\Rightarrow{min}\left({p}\right)=\mathrm{2} \\ $$$$ \\ $$$${if}\:{p}=\mathrm{2}\Rightarrow{r}=\mathrm{1} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −{qx}+\mathrm{1}=\mathrm{0}\Rightarrow{q}>\mathrm{2}\sqrt{\mathrm{2}}\Rightarrow{min}\left({q}\right)=\mathrm{3} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}=\mathrm{0}\:{has}\:{two}\:{distict}\:{root}\:\mathrm{1},\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
