Question Number 117555 by dw last updated on 12/Oct/20

$${Alternative}\:{forms} \\ $$$$\begin{cases}{\sqrt{{x}}+\sqrt{{y}}=\frac{\mathrm{23}}{\mathrm{12}}}\\{\mathrm{9}{x}+\mathrm{16}{y}=\mathrm{29}}\end{cases} \\ $$$$ \\ $$
Answered by Olaf last updated on 12/Oct/20
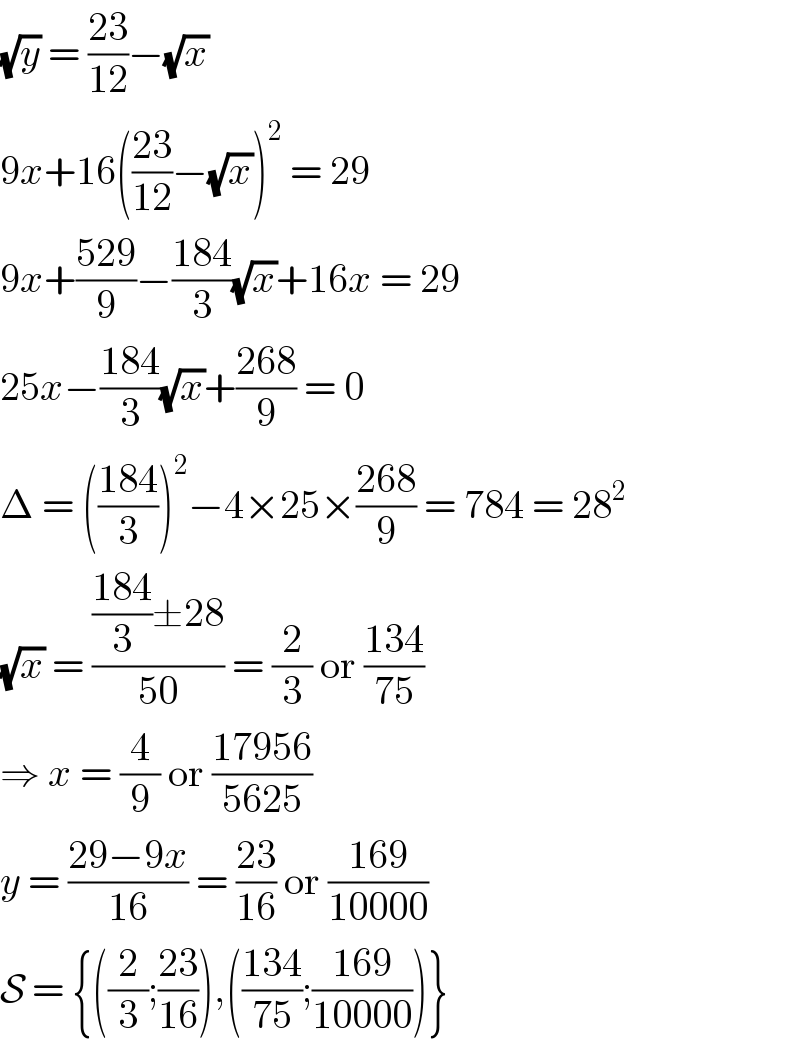
$$\sqrt{{y}}\:=\:\frac{\mathrm{23}}{\mathrm{12}}−\sqrt{{x}} \\ $$$$\mathrm{9}{x}+\mathrm{16}\left(\frac{\mathrm{23}}{\mathrm{12}}−\sqrt{{x}}\right)^{\mathrm{2}} \:=\:\mathrm{29} \\ $$$$\mathrm{9}{x}+\frac{\mathrm{529}}{\mathrm{9}}−\frac{\mathrm{184}}{\mathrm{3}}\sqrt{{x}}+\mathrm{16}{x}\:=\:\mathrm{29} \\ $$$$\mathrm{25}{x}−\frac{\mathrm{184}}{\mathrm{3}}\sqrt{{x}}+\frac{\mathrm{268}}{\mathrm{9}}\:=\:\mathrm{0} \\ $$$$\Delta\:=\:\left(\frac{\mathrm{184}}{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{25}×\frac{\mathrm{268}}{\mathrm{9}}\:=\:\mathrm{784}\:=\:\mathrm{28}^{\mathrm{2}} \\ $$$$\sqrt{{x}}\:=\:\frac{\frac{\mathrm{184}}{\mathrm{3}}\pm\mathrm{28}}{\mathrm{50}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{or}\:\frac{\mathrm{134}}{\mathrm{75}} \\ $$$$\Rightarrow\:{x}\:=\:\frac{\mathrm{4}}{\mathrm{9}}\:\mathrm{or}\:\frac{\mathrm{17956}}{\mathrm{5625}} \\ $$$${y}\:=\:\frac{\mathrm{29}−\mathrm{9}{x}}{\mathrm{16}}\:=\:\frac{\mathrm{23}}{\mathrm{16}}\:\mathrm{or}\:\frac{\mathrm{169}}{\mathrm{10000}} \\ $$$$\mathcal{S}\:=\:\left\{\left(\frac{\mathrm{2}}{\mathrm{3}};\frac{\mathrm{23}}{\mathrm{16}}\right),\left(\frac{\mathrm{134}}{\mathrm{75}};\frac{\mathrm{169}}{\mathrm{10000}}\right)\right\} \\ $$
Answered by Olaf last updated on 12/Oct/20
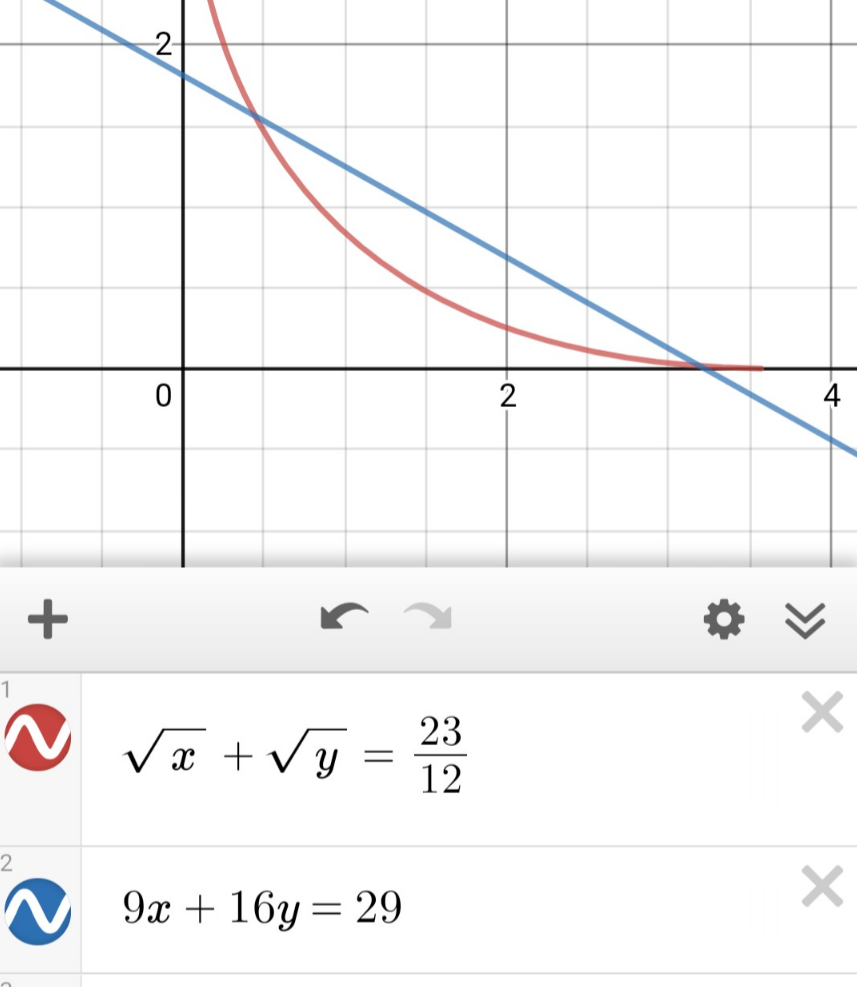
Commented by Olaf last updated on 12/Oct/20

$$\mathrm{2}\:\mathrm{solutions}. \\ $$
