Question Number 154291 by joki last updated on 16/Sep/21
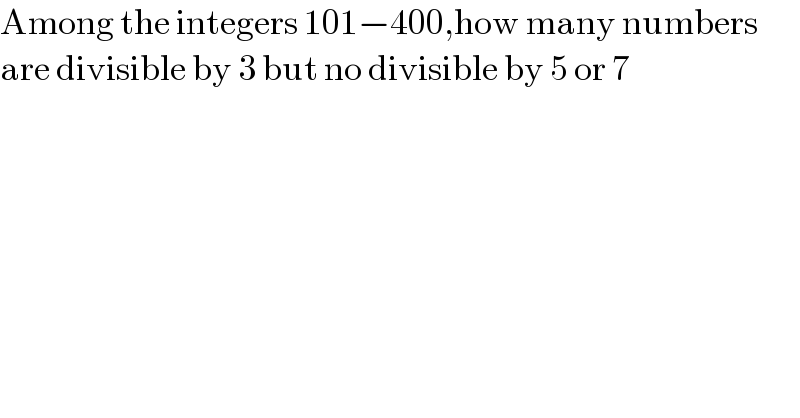
$$\mathrm{Among}\:\mathrm{the}\:\mathrm{integers}\:\mathrm{101}−\mathrm{400},\mathrm{how}\:\mathrm{many}\:\mathrm{numbers} \\ $$$$\mathrm{are}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3}\:\mathrm{but}\:\mathrm{no}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{5}\:\mathrm{or}\:\mathrm{7} \\ $$
Answered by talminator2856791 last updated on 16/Sep/21
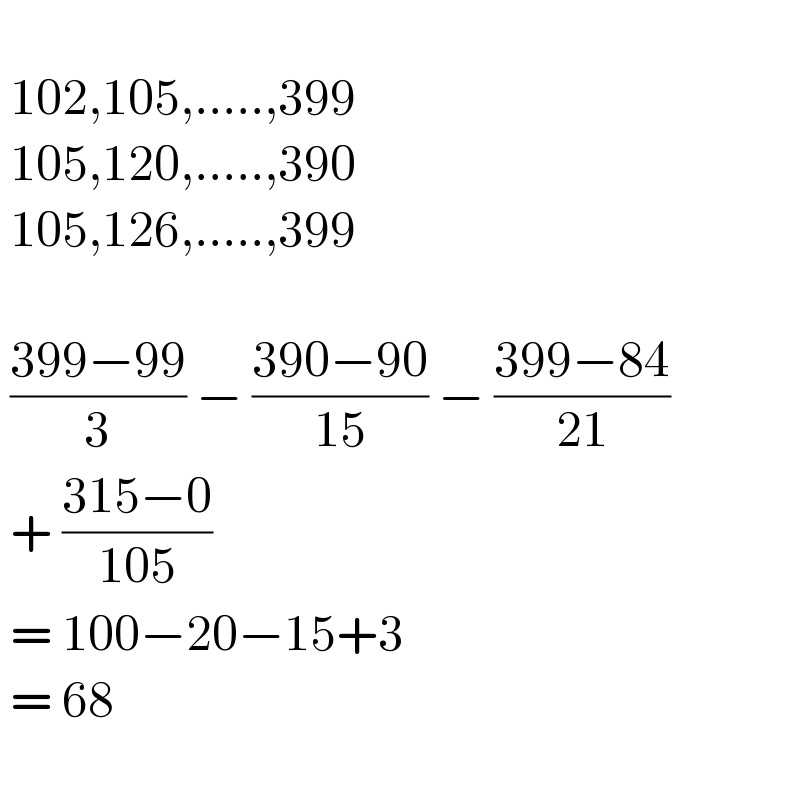
$$\: \\ $$$$\:\mathrm{102},\mathrm{105},…..,\mathrm{399} \\ $$$$\:\mathrm{105},\mathrm{120},…..,\mathrm{390} \\ $$$$\:\mathrm{105},\mathrm{126},…..,\mathrm{399} \\ $$$$\: \\ $$$$\:\frac{\mathrm{399}−\mathrm{99}}{\mathrm{3}}\:−\:\frac{\mathrm{390}−\mathrm{90}}{\mathrm{15}}\:−\:\frac{\mathrm{399}−\mathrm{84}}{\mathrm{21}} \\ $$$$\:+\:\frac{\mathrm{315}−\mathrm{0}}{\mathrm{105}}\: \\ $$$$\:=\:\mathrm{100}−\mathrm{20}−\mathrm{15}+\mathrm{3} \\ $$$$\:=\:\mathrm{68} \\ $$$$\: \\ $$
Answered by mr W last updated on 16/Sep/21
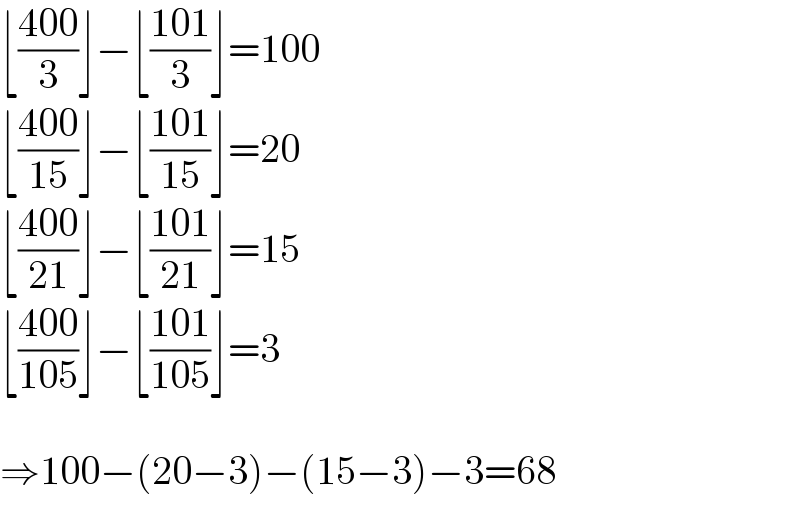
$$\lfloor\frac{\mathrm{400}}{\mathrm{3}}\rfloor−\lfloor\frac{\mathrm{101}}{\mathrm{3}}\rfloor=\mathrm{100} \\ $$$$\lfloor\frac{\mathrm{400}}{\mathrm{15}}\rfloor−\lfloor\frac{\mathrm{101}}{\mathrm{15}}\rfloor=\mathrm{20} \\ $$$$\lfloor\frac{\mathrm{400}}{\mathrm{21}}\rfloor−\lfloor\frac{\mathrm{101}}{\mathrm{21}}\rfloor=\mathrm{15} \\ $$$$\lfloor\frac{\mathrm{400}}{\mathrm{105}}\rfloor−\lfloor\frac{\mathrm{101}}{\mathrm{105}}\rfloor=\mathrm{3} \\ $$$$ \\ $$$$\Rightarrow\mathrm{100}−\left(\mathrm{20}−\mathrm{3}\right)−\left(\mathrm{15}−\mathrm{3}\right)−\mathrm{3}=\mathrm{68} \\ $$
