Question Number 119035 by ZiYangLee last updated on 21/Oct/20
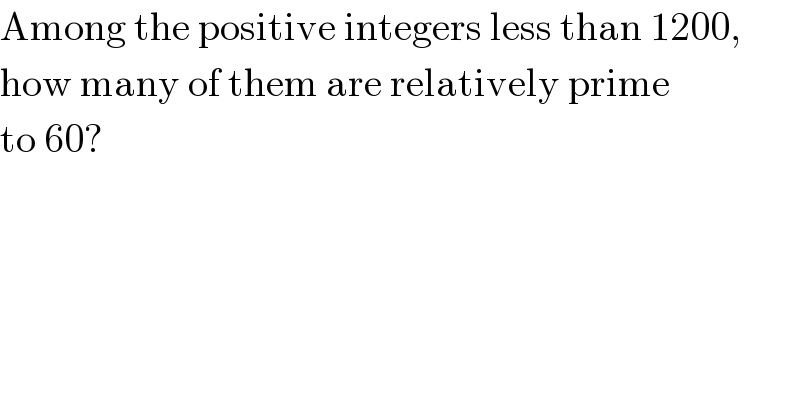
$$\mathrm{Among}\:\mathrm{the}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{less}\:\mathrm{than}\:\mathrm{1200}, \\ $$$$\mathrm{how}\:\mathrm{many}\:\mathrm{of}\:\mathrm{them}\:\mathrm{are}\:\mathrm{relatively}\:\mathrm{prime} \\ $$$$\mathrm{to}\:\mathrm{60}? \\ $$
Answered by floor(10²Eta[1]) last updated on 21/Oct/20

$$\mathrm{60}=\mathrm{2}^{\mathrm{2}} .\mathrm{3}.\mathrm{5} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{how}\:\mathrm{many}\:\mathrm{numbers} \\ $$$$\mathrm{that}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{have}\:\mathrm{2},\:\mathrm{3}\:\mathrm{or}\:\mathrm{5}\:\mathrm{as}\:\mathrm{factors}\: \\ $$$$\mathrm{1200}−\lfloor\frac{\mathrm{1200}}{\mathrm{2}}\rfloor=\mathrm{600}\:\mathrm{numbers}\:\mathrm{that}\:\mathrm{are}\:\mathrm{not} \\ $$$$\mathrm{divisible}\:\mathrm{by}\:\mathrm{2}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{1200} \\ $$$$\mathrm{600}−\lfloor\frac{\mathrm{600}}{\mathrm{3}}\rfloor=\mathrm{400}\:\mathrm{numbers}\:\mathrm{that}\:\mathrm{don}'\mathrm{t}\:\mathrm{have} \\ $$$$\mathrm{factor}\:\mathrm{3}\:\mathrm{or}\:\mathrm{2}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{1200} \\ $$$$\mathrm{400}−\lfloor\frac{\mathrm{400}}{\mathrm{5}}\rfloor=\mathrm{320}\:\mathrm{numbers}\:\mathrm{that}\:\mathrm{doesn}'\mathrm{t}\: \\ $$$$\mathrm{have}\:\mathrm{factors}\:\mathrm{2},\:\mathrm{3}\:\mathrm{or}\:\mathrm{5}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{1200} \\ $$$$\mathrm{Answer}:\:\mathrm{320} \\ $$
Commented by ZiYangLee last updated on 22/Oct/20

$$\bigstar\bigstar \\ $$
