Menu Close

An-aeroplane-has-to-go-from-a-point-A-to-point-B-500-km-away-due-30-east-of-north-A-wind-is-blowing-due-north-at-a-speed-of-20-ms-1-The-air-speed-of-the-plane-is-150-ms-1-Find-the-directi

Tinku Tara 0 Comments
Pin




Question Number 19986 by Tinkutara last updated on 19/Aug/17
An aeroplane has to go from a point A to point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 ms^(−1) . The air speed of the plane is 150 ms^(−1) . Find the direction in which the pilot should head the plane to reach point B.
$$\mathrm{An}\:\mathrm{aeroplane}\:\mathrm{has}\:\mathrm{to}\:\mathrm{go}\:\mathrm{from}\:\mathrm{a}\:\mathrm{point}\:{A} \\ $$$$\mathrm{to}\:\mathrm{point}\:{B},\:\mathrm{500}\:\mathrm{km}\:\mathrm{away}\:\mathrm{due}\:\mathrm{30}°\:\mathrm{east} \\ $$$$\mathrm{of}\:\mathrm{north}.\:\mathrm{A}\:\mathrm{wind}\:\mathrm{is}\:\mathrm{blowing}\:\mathrm{due}\:\mathrm{north} \\ $$$$\mathrm{at}\:\mathrm{a}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{20}\:\mathrm{ms}^{−\mathrm{1}} .\:\mathrm{The}\:\mathrm{air}\:\mathrm{speed}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{plane}\:\mathrm{is}\:\mathrm{150}\:\mathrm{ms}^{−\mathrm{1}} .\:\mathrm{Find}\:\mathrm{the}\:\mathrm{direction} \\ $$$$\mathrm{in}\:\mathrm{which}\:\mathrm{the}\:\mathrm{pilot}\:\mathrm{should}\:\mathrm{head}\:\mathrm{the} \\ $$$$\mathrm{plane}\:\mathrm{to}\:\mathrm{reach}\:\mathrm{point}\:{B}. \\ $$
Answered by ajfour last updated on 19/Aug/17
θ=sin^(−1) ((1/(15))) east of AB. which means 30°+sin^(−1) ((1/(15))) east of north. air speed i assume to be speed of plane when no wind blows.
$$\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{15}}\right)\:\:{east}\:{of}\:{AB}. \\ $$$${which}\:{means}\:\mathrm{30}°+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{15}}\right)\:{east} \\ $$$${of}\:{north}. \\ $$$${air}\:{speed}\:{i}\:{assume}\:{to}\:{be}\:{speed}\:{of} \\ $$$${plane}\:{when}\:{no}\:{wind}\:{blows}. \\ $$
Commented by ajfour last updated on 20/Aug/17
Commented by mrW1 last updated on 20/Aug/17
what is the time the plane needs to reach B?
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{time}\:\mathrm{the}\:\mathrm{plane}\:\mathrm{needs}\:\mathrm{to} \\ $$$$\mathrm{reach}\:\mathrm{B}? \\ $$
Commented by ajfour last updated on 20/Aug/17
t=(d/(wcos 30°+vcos θ)) =((500km)/((20(((√3)/2))+150(√(1−(1/(225)))) )m/s)) ≈((500)/(((18)/5)(10(√3)+150(1−(1/(450))))) h =((500)/(36(√3)+540−1.2)) h =((500)/(601.152)) s ≈ 50 min . without the wind it would have taken t_0 =((500)/((((18)/5)×150)))= ((500)/(540)) h ≈((25)/(27)) h t_0 =((25)/(3×9))×60 =55.5min .
$${t}=\frac{{d}}{{w}\mathrm{cos}\:\mathrm{30}°+{v}\mathrm{cos}\:\theta} \\ $$$$\:=\frac{\mathrm{500}{km}}{\left(\mathrm{20}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\mathrm{150}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{225}}}\:\right){m}/{s}} \\ $$$$\:\:\:\:\approx\frac{\mathrm{500}}{\frac{\mathrm{18}}{\mathrm{5}}\left(\mathrm{10}\sqrt{\mathrm{3}}+\mathrm{150}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{450}}\right)\right.}\:{h} \\ $$$$\:\:\:\:\:=\frac{\mathrm{500}}{\mathrm{36}\sqrt{\mathrm{3}}+\mathrm{540}−\mathrm{1}.\mathrm{2}}\:{h} \\ $$$$\:\:\:\:\:=\frac{\mathrm{500}}{\mathrm{601}.\mathrm{152}}\:{s}\:\approx\:\mathrm{50}\:\boldsymbol{{min}}\:. \\ $$$${without}\:{the}\:{wind}\:{it}\:{would}\:{have} \\ $$$${taken}\:{t}_{\mathrm{0}} =\frac{\mathrm{500}}{\left(\frac{\mathrm{18}}{\mathrm{5}}×\mathrm{150}\right)}=\:\frac{\mathrm{500}}{\mathrm{540}}\:{h}\:\approx\frac{\mathrm{25}}{\mathrm{27}}\:{h} \\ $$$$\:\:\:\:\:{t}_{\mathrm{0}} =\frac{\mathrm{25}}{\mathrm{3}×\mathrm{9}}×\mathrm{60}\:=\mathrm{55}.\mathrm{5}{min}\:. \\ $$
Commented by Tinkutara last updated on 20/Aug/17
Thank you very much Sir! That was the next part.
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}!\:\mathrm{That}\:\mathrm{was} \\ $$$$\mathrm{the}\:\mathrm{next}\:\mathrm{part}. \\ $$
Commented by Tinkutara last updated on 26/Aug/17
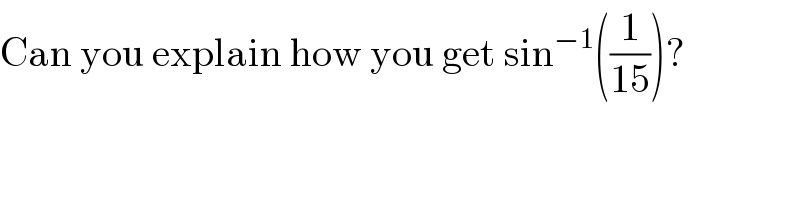
Can you explain how you get sin^(−1) ((1/(15)))?
$$\mathrm{Can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{15}}\right)? \\ $$
Commented by ajfour last updated on 26/Aug/17
the transverse component (⊥ to AB) of wind velocity=10m/s needs to be cancelled by component of plane′s velocity; the plane heads forward in such a direction⇒ sin θ=((20cos 60°)/(150)) =(1/(15)) .
$${the}\:{transverse}\:{component} \\ $$$$\left(\bot\:{to}\:{AB}\right)\:{of}\:{wind}\:{velocity}=\mathrm{10}{m}/{s} \\ $$$${needs}\:{to}\:{be}\:{cancelled}\:{by}\:{component} \\ $$$${of}\:{plane}'{s}\:{velocity};\:{the}\:{plane}\:{heads} \\ $$$${forward}\:{in}\:{such}\:{a}\:{direction}\Rightarrow \\ $$$$\:\mathrm{sin}\:\theta=\frac{\mathrm{20cos}\:\mathrm{60}°}{\mathrm{150}}\:=\frac{\mathrm{1}}{\mathrm{15}}\:. \\ $$
Commented by Tinkutara last updated on 26/Aug/17
Thank you very much Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *