Question Number 47333 by Necxx last updated on 08/Nov/18

$${An}\:{aircraft}\:{flying}\:{horizontally} \\ $$$$\mathrm{100}{m}\:{above}\:{the}\:{ground}\:{and}\:{at}\:\mathrm{720}{km}/{h} \\ $$$${drops}\:{a}\:{bomb}\:{on}\:{a}\:{target}\:{on}\:{the} \\ $$$${ground}.{Determine}\:{the}\:{acute}\:{angle} \\ $$$${between}\:{the}\:{vertical}\:{and}\:{the}\:{line} \\ $$$${joining}\:{the}\:{aircraft}\:{and}\:{target}\:{at} \\ $$$${the}\:{instance}\:{when}\:{the}\:{bomb}\:{is} \\ $$$${released}.\left({g}=\mathrm{10}{ms}^{−\mathrm{2}} \right) \\ $$$$ \\ $$
Answered by MrW3 last updated on 08/Nov/18

$${v}=\mathrm{720}{km}/{h}=\mathrm{200}{m}/{s} \\ $$$${x}={vt} \\ $$$${y}=\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}\Rightarrow{t}=\sqrt{\frac{\mathrm{2}{y}}{{g}}} \\ $$$$\Rightarrow{x}={v}\sqrt{\frac{\mathrm{2}{y}}{{g}}} \\ $$$$\mathrm{tan}\:\theta=\frac{{x}}{{y}}={v}\sqrt{\frac{\mathrm{2}}{{gy}}}=\mathrm{200}\sqrt{\frac{\mathrm{2}}{\mathrm{10}×\mathrm{100}}}=\frac{\mathrm{20}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{20}}{\:\sqrt{\mathrm{5}}}=\mathrm{83}.\mathrm{6}° \\ $$
Commented by Necxx last updated on 08/Nov/18
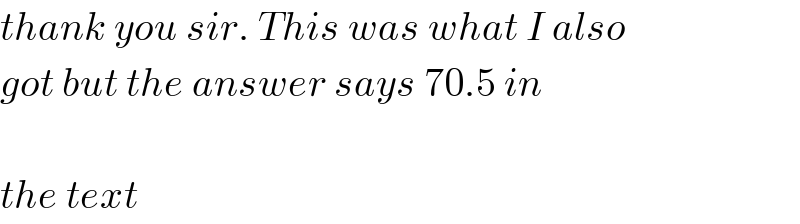
$${thank}\:{you}\:{sir}.\:{This}\:{was}\:{what}\:{I}\:{also} \\ $$$${got}\:{but}\:{the}\:{answer}\:{says}\:\mathrm{70}.\mathrm{5}\:{in} \\ $$$$ \\ $$$${the}\:{text} \\ $$
Commented by MrW3 last updated on 08/Nov/18
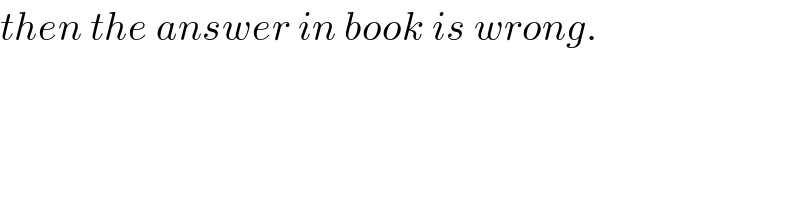
$${then}\:{the}\:{answer}\:{in}\:{book}\:{is}\:{wrong}. \\ $$
Answered by ajfour last updated on 08/Nov/18
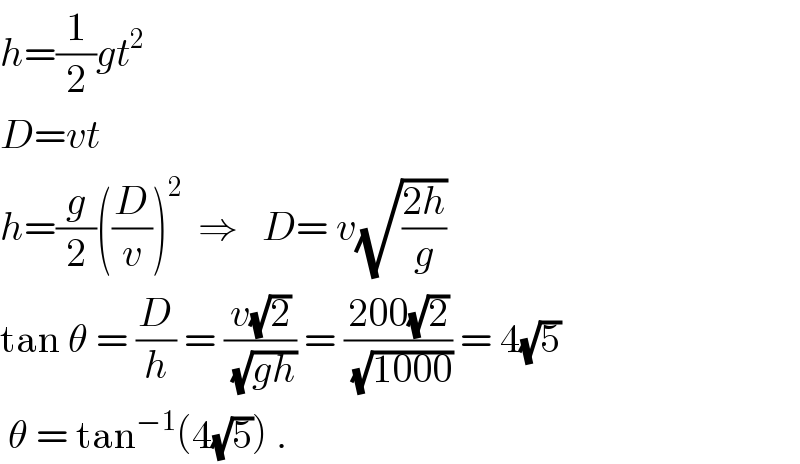
$${h}=\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${D}={vt} \\ $$$${h}=\frac{{g}}{\mathrm{2}}\left(\frac{{D}}{{v}}\right)^{\mathrm{2}} \:\:\Rightarrow\:\:\:{D}=\:{v}\sqrt{\frac{\mathrm{2}{h}}{{g}}}\: \\ $$$$\mathrm{tan}\:\theta\:=\:\frac{{D}}{{h}}\:=\:\frac{{v}\sqrt{\mathrm{2}}}{\:\sqrt{{gh}}}\:=\:\frac{\mathrm{200}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{1000}}}\:=\:\mathrm{4}\sqrt{\mathrm{5}}\: \\ $$$$\:\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{4}\sqrt{\mathrm{5}}\right)\:. \\ $$
