Question Number 90709 by Cynosure last updated on 25/Apr/20
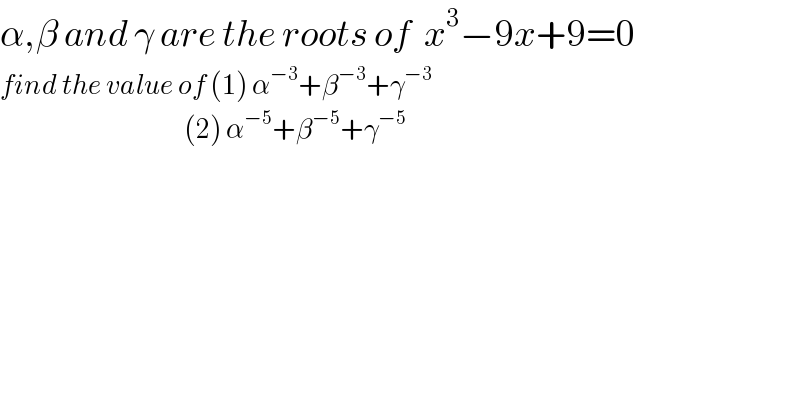
$$\alpha,\beta\:{and}\:\gamma\:{are}\:{the}\:{roots}\:{of}\:\:{x}^{\mathrm{3}} −\mathrm{9}{x}+\mathrm{9}=\mathrm{0} \\ $$$${find}\:{the}\:{value}\:{of}\:\left(\mathrm{1}\right)\:\alpha^{−\mathrm{3}} +\beta^{−\mathrm{3}} +\gamma^{−\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right)\:\alpha^{−\mathrm{5}} +\beta^{−\mathrm{5}} +\gamma^{−\mathrm{5}} \\ $$
Commented by jagoll last updated on 25/Apr/20
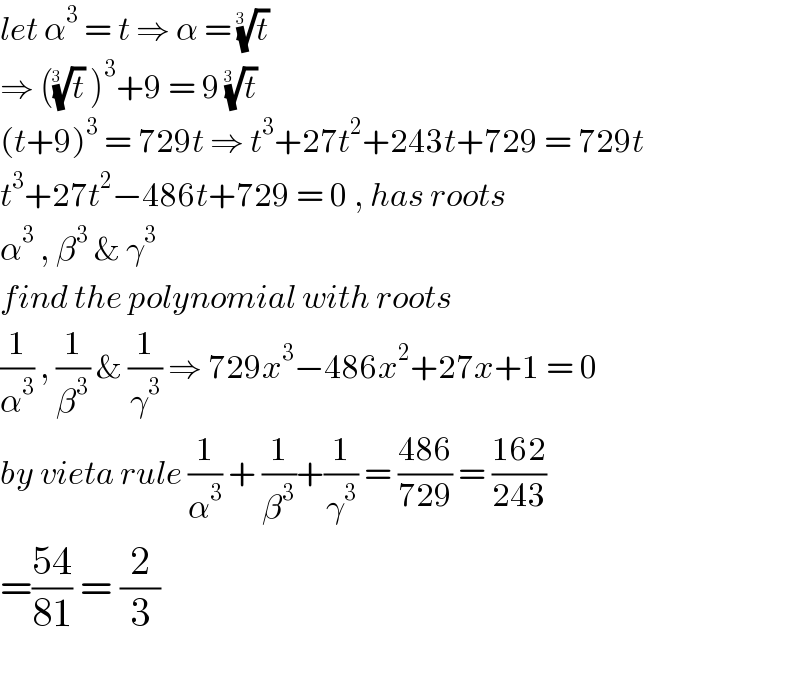
$${let}\:\alpha^{\mathrm{3}} \:=\:{t}\:\Rightarrow\:\alpha\:=\:\sqrt[{\mathrm{3}\:\:}]{{t}} \\ $$$$\Rightarrow\:\left(\sqrt[{\mathrm{3}\:\:}]{{t}}\:\right)^{\mathrm{3}} +\mathrm{9}\:=\:\mathrm{9}\:\sqrt[{\mathrm{3}\:\:}]{{t}} \\ $$$$\left({t}+\mathrm{9}\right)^{\mathrm{3}} \:=\:\mathrm{729}{t}\:\Rightarrow\:{t}^{\mathrm{3}} +\mathrm{27}{t}^{\mathrm{2}} +\mathrm{243}{t}+\mathrm{729}\:=\:\mathrm{729}{t} \\ $$$${t}^{\mathrm{3}} +\mathrm{27}{t}^{\mathrm{2}} −\mathrm{486}{t}+\mathrm{729}\:=\:\mathrm{0}\:,\:{has}\:{roots} \\ $$$$\alpha^{\mathrm{3}} \:,\:\beta^{\mathrm{3}} \:\&\:\gamma^{\mathrm{3}} \\ $$$${find}\:{the}\:{polynomial}\:{with}\:{roots} \\ $$$$\frac{\mathrm{1}}{\alpha^{\mathrm{3}} }\:,\:\frac{\mathrm{1}}{\beta^{\mathrm{3}} }\:\&\:\frac{\mathrm{1}}{\gamma^{\mathrm{3}} }\:\Rightarrow\:\mathrm{729}{x}^{\mathrm{3}} −\mathrm{486}{x}^{\mathrm{2}} +\mathrm{27}{x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$${by}\:{vieta}\:{rule}\:\frac{\mathrm{1}}{\alpha^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\beta^{\mathrm{3}} }+\frac{\mathrm{1}}{\gamma^{\mathrm{3}} }\:=\:\frac{\mathrm{486}}{\mathrm{729}}\:=\:\frac{\mathrm{162}}{\mathrm{243}} \\ $$$$=\frac{\mathrm{54}}{\mathrm{81}}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$
Commented by Cynosure last updated on 25/Apr/20
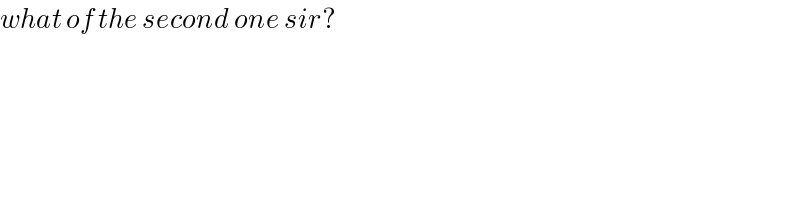
$${what}\:{of}\:{the}\:{second}\:{one}\:{sir}? \\ $$
