Question Number 79757 by mathocean1 last updated on 27/Jan/20

$$\mathrm{And}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{is} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}{y}=\mathrm{0}. \\ $$$$\left({T}\right)\:\mathrm{is}\:\mathrm{his}\:\mathrm{his}\:\mathrm{tangent}\:\mathrm{line}\:\mathrm{at}\:\mathrm{M}\left({x}_{\mathrm{0}} ;{y}_{\mathrm{0}} \right) \\ $$$${passing}\:{by}\:{D}\left(\mathrm{2};\mathrm{1}\right). \\ $$$$ \\ $$$$\left.\mathrm{a}\right)\:\mathrm{Show}\:\mathrm{that}\:\mathrm{y}\:\mathrm{verify}\:\mathrm{y}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{y}_{\mathrm{0}} =\mathrm{0} \\ $$$$\left.\mathrm{b}\right)\:\mathrm{deduct}\:\mathrm{others}\:\mathrm{tangent}'\mathrm{s}\: \\ $$$$\mathrm{equations}\:\mathrm{to}\:\mathrm{Circle}\:\mathrm{passing}\:\mathrm{by}\:\mathrm{D}. \\ $$
Commented by john santu last updated on 27/Jan/20
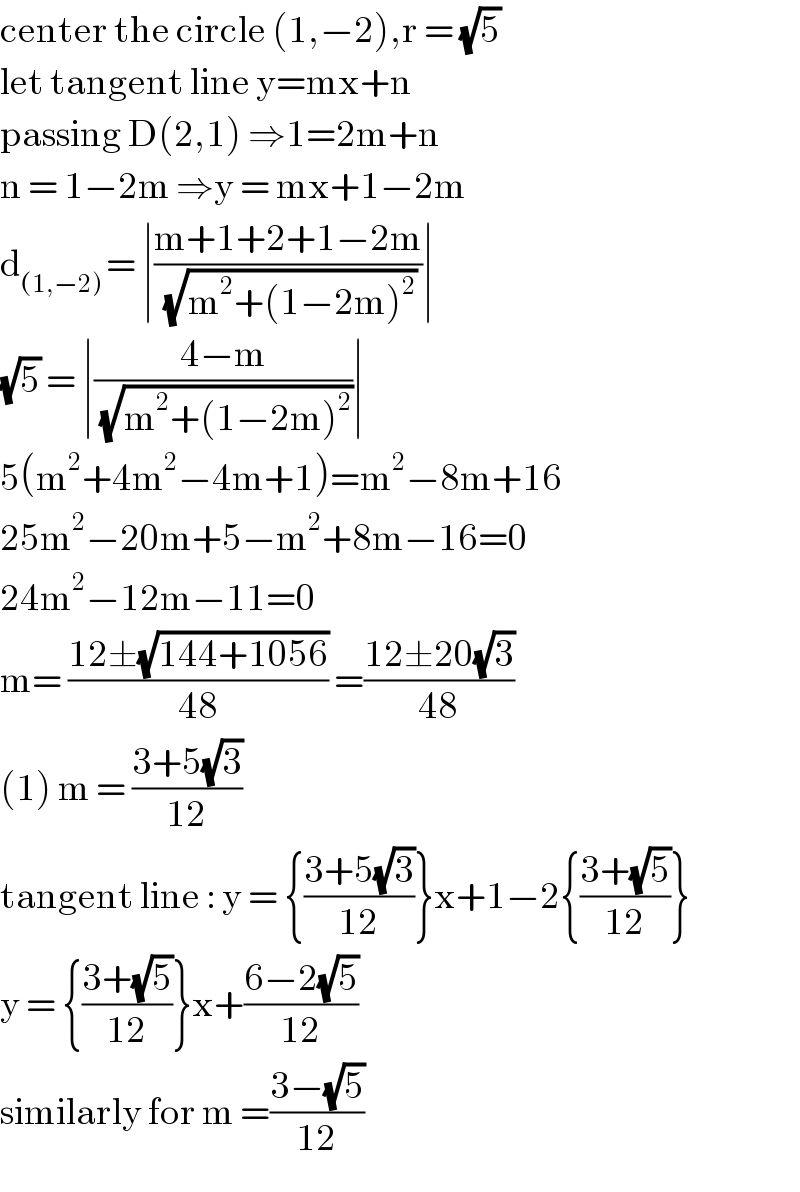
$$\mathrm{center}\:\mathrm{the}\:\mathrm{circle}\:\left(\mathrm{1},−\mathrm{2}\right),\mathrm{r}\:=\:\sqrt{\mathrm{5}} \\ $$$$\mathrm{let}\:\mathrm{tangent}\:\mathrm{line}\:\mathrm{y}=\mathrm{mx}+\mathrm{n} \\ $$$$\mathrm{passing}\:\mathrm{D}\left(\mathrm{2},\mathrm{1}\right)\:\Rightarrow\mathrm{1}=\mathrm{2m}+\mathrm{n} \\ $$$$\mathrm{n}\:=\:\mathrm{1}−\mathrm{2m}\:\Rightarrow\mathrm{y}\:=\:\mathrm{mx}+\mathrm{1}−\mathrm{2m} \\ $$$$\mathrm{d}_{\left(\mathrm{1},−\mathrm{2}\right)\:} =\:\mid\frac{\mathrm{m}+\mathrm{1}+\mathrm{2}+\mathrm{1}−\mathrm{2m}}{\:\sqrt{\mathrm{m}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{2m}\right)^{\mathrm{2}} }}\mid \\ $$$$\sqrt{\mathrm{5}}\:=\:\mid\frac{\mathrm{4}−\mathrm{m}}{\:\sqrt{\mathrm{m}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{2m}\right)^{\mathrm{2}} }}\mid \\ $$$$\mathrm{5}\left(\mathrm{m}^{\mathrm{2}} +\mathrm{4m}^{\mathrm{2}} −\mathrm{4m}+\mathrm{1}\right)=\mathrm{m}^{\mathrm{2}} −\mathrm{8m}+\mathrm{16} \\ $$$$\mathrm{25m}^{\mathrm{2}} −\mathrm{20m}+\mathrm{5}−\mathrm{m}^{\mathrm{2}} +\mathrm{8m}−\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{24m}^{\mathrm{2}} −\mathrm{12m}−\mathrm{11}=\mathrm{0} \\ $$$$\mathrm{m}=\:\frac{\mathrm{12}\pm\sqrt{\mathrm{144}+\mathrm{1056}}}{\mathrm{48}}\:=\frac{\mathrm{12}\pm\mathrm{20}\sqrt{\mathrm{3}}}{\mathrm{48}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{m}\:=\:\frac{\mathrm{3}+\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{12}} \\ $$$$\mathrm{tangent}\:\mathrm{line}\::\:\mathrm{y}\:=\:\left\{\frac{\mathrm{3}+\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{12}}\right\}\mathrm{x}+\mathrm{1}−\mathrm{2}\left\{\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{12}}\right\} \\ $$$$\mathrm{y}\:=\:\left\{\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{12}}\right\}\mathrm{x}+\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{12}} \\ $$$$\mathrm{similarly}\:\mathrm{for}\:\mathrm{m}\:=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{12}} \\ $$
