Question Number 79085 by key of knowledge last updated on 22/Jan/20
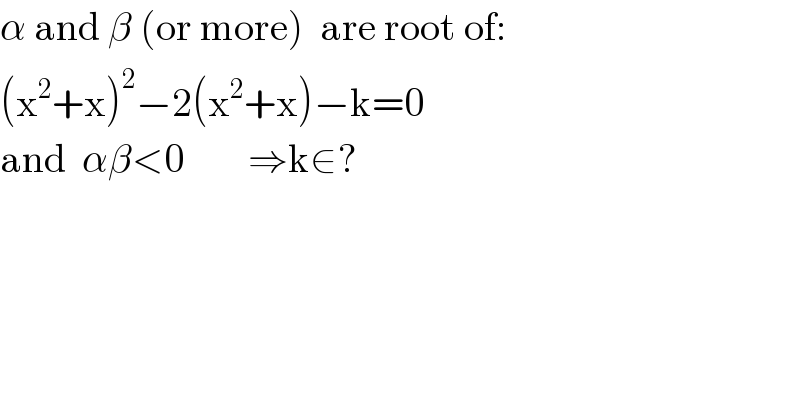
$$\alpha\:\mathrm{and}\:\beta\:\left(\mathrm{or}\:\mathrm{more}\right)\:\:\mathrm{are}\:\mathrm{root}\:\mathrm{of}: \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)−\mathrm{k}=\mathrm{0} \\ $$$$\mathrm{and}\:\:\alpha\beta<\mathrm{0}\:\:\:\:\:\:\:\:\Rightarrow\mathrm{k}\in? \\ $$
Commented by mr W last updated on 22/Jan/20

$${k}\in\left[−\mathrm{1},\mathrm{0}\right) \\ $$$${right}? \\ $$
Answered by MJS last updated on 23/Jan/20

$$\left({x}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} −\mathrm{2}\left({x}^{\mathrm{2}} +{x}\right)−{k}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{2}} +{x}=\mathrm{1}\pm\sqrt{{k}+\mathrm{1}} \\ $$$$\Rightarrow \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}+\mathrm{4}\sqrt{{k}+\mathrm{1}}}}{\mathrm{2}}\vee{x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}−\mathrm{4}\sqrt{{k}+\mathrm{1}}}}{\mathrm{2}} \\ $$$$\mathrm{to}\:\mathrm{get}\:\mathrm{4}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$−\mathrm{1}\leqslant{k}\leqslant\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\mathrm{for}\:{k}\geqslant−\mathrm{1}\:\mathrm{there}'\mathrm{s}\:\mathrm{always}\:\mathrm{a}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{roots}\:\alpha,\:\beta \\ $$$$\mathrm{with}\:\alpha\beta<\mathrm{0} \\ $$
