Menu Close

answer-to26109-S-n-k-1-k-n-1-k-2-k-1-2-we-decompose-F-X-1-X-2-X-1-2-a-X-b-X-2-c-X-1-d-X-1-2-we-find-F-X-2-X-1-X-2-2-X-

Tinku Tara 0 Comments
Pin




Question Number 26121 by abdo imad last updated on 20/Dec/17
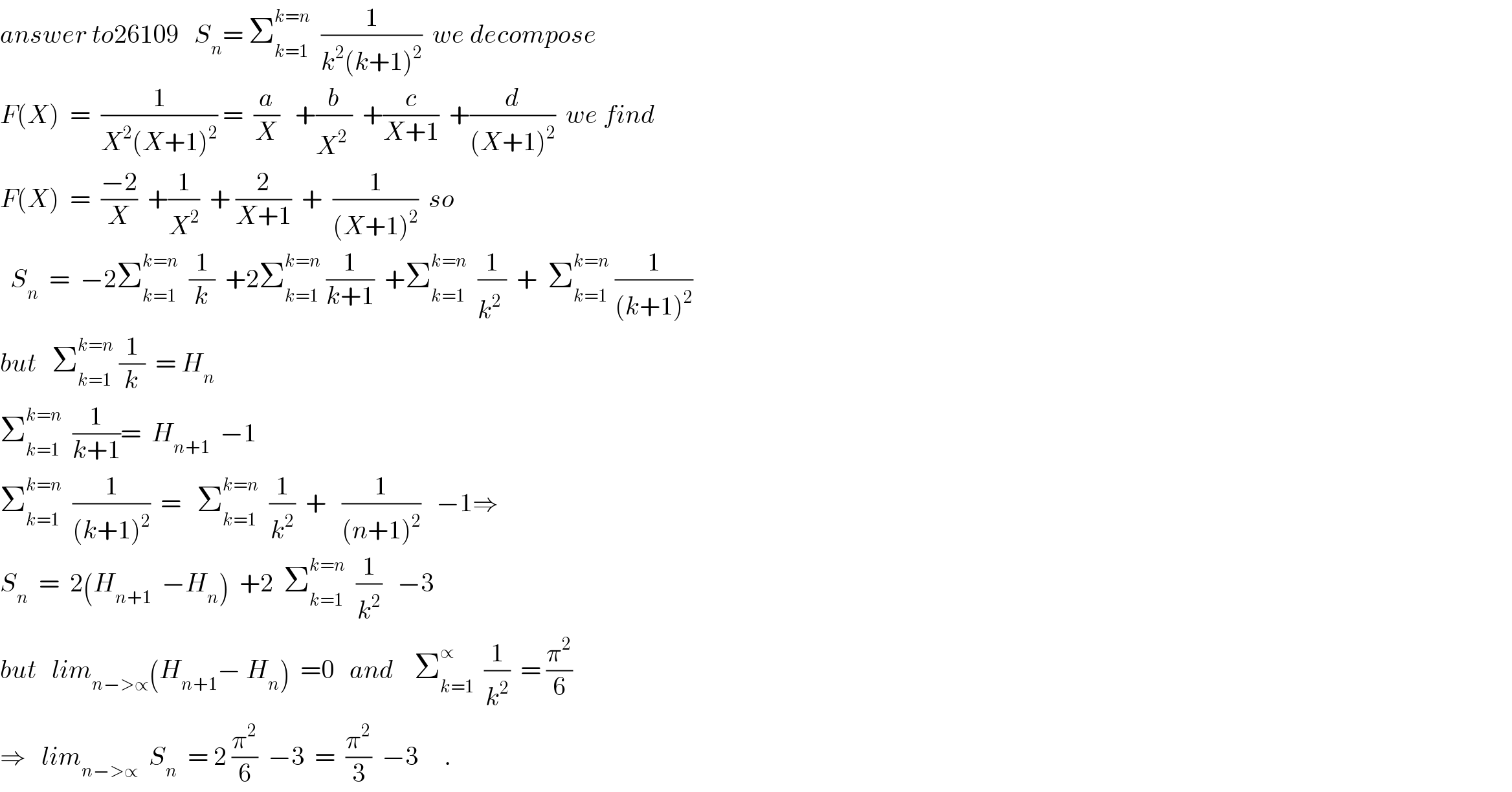
answer to26109 S_n = Σ_(k=1) ^(k=n) (1/(k^2 (k+1)^2 )) we decompose F(X) = (1/(X^2 (X+1)^2 )) = (a/X) +(b/X^2^ ) +(c/(X+1)) +(d/((X+1)^2 )) we find F(X) = ((−2)/X) +(1/X^2 ) + (2/(X+1)) + (1/((X+1)^2 )) so S_n = −2Σ_(k=1) ^(k=n) (1/k) +2Σ_(k=1) ^(k=n) (1/(k+1)) +Σ_(k=1) ^(k=n) (1/k^2^ ) + Σ_(k=1) ^(k=n) (1/((k+1)^2 )) but Σ_(k=1) ^(k=n) (1/k) = H_n Σ_(k=1) ^(k=n) (1/(k+1))= H_(n+1) −1 Σ_(k=1) ^(k=n) (1/((k+1)^2 )) = Σ_(k=1) ^(k=n) (1/k^2 ) + (1/((n+1)^2 )) −1⇒ S_n = 2(H_(n+1) −H_n ) +2 Σ_(k=1) ^(k=n) (1/k^2 ) −3 but lim_(n−>∝) (H_(n+1) − H_n ) =0 and Σ_(k=1) ^∝ (1/k^2 ) = (π^2 /6) ⇒ lim_(n−>∝) S_n = 2 (π^2 /6) −3 = (π^2 /3) −3 .
$${answer}\:{to}\mathrm{26109}\:\:\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:\:{we}\:{decompose} \\ $$$${F}\left({X}\right)\:\:=\:\:\frac{\mathrm{1}}{{X}^{\mathrm{2}} \left({X}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\:\frac{{a}}{{X}}\:\:\:+\frac{{b}}{{X}^{\mathrm{2}^{} } }\:\:+\frac{{c}}{{X}+\mathrm{1}}\:\:+\frac{{d}}{\left({X}+\mathrm{1}\right)^{\mathrm{2}} }\:\:{we}\:{find} \\ $$$${F}\left({X}\right)\:\:=\:\:\frac{−\mathrm{2}}{{X}}\:\:+\frac{\mathrm{1}}{{X}^{\mathrm{2}} }\:\:+\:\frac{\mathrm{2}}{{X}+\mathrm{1}}\:\:+\:\:\frac{\mathrm{1}}{\left({X}+\mathrm{1}\right)^{\mathrm{2}} }\:\:{so} \\ $$$$\:\:{S}_{{n}} \:\:=\:\:−\mathrm{2}\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\frac{\mathrm{1}}{{k}}\:\:+\mathrm{2}\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:\:+\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}^{} } }\:\:+\:\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${but}\:\:\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\frac{\mathrm{1}}{{k}}\:\:=\:{H}_{{n}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\frac{\mathrm{1}}{{k}+\mathrm{1}}=\:\:{H}_{{n}+\mathrm{1}} \:\:−\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:\:=\:\:\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:\:+\:\:\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:−\mathrm{1}\Rightarrow \\ $$$${S}_{{n}} \:\:=\:\:\mathrm{2}\left({H}_{{n}+\mathrm{1}} \:\:−{H}_{{n}} \right)\:\:+\mathrm{2}\:\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:\:\:−\mathrm{3} \\ $$$${but}\:\:\:{lim}_{{n}−>\propto} \left({H}_{{n}+\mathrm{1}} −\:{H}_{{n}} \right)\:\:=\mathrm{0}\:\:\:{and}\:\:\:\:\sum_{{k}=\mathrm{1}} ^{\propto} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\Rightarrow\:\:\:{lim}_{{n}−>\propto} \:\:{S}_{{n}} \:\:=\:\mathrm{2}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:−\mathrm{3}\:\:=\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\:\:−\mathrm{3}\:\:\:\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *