Question Number 170995 by Mastermind last updated on 05/Jun/22

$${Approximate}\:{sin}\mathrm{46}°\:{by}\:“{differentials}'' \\ $$$$ \\ $$$${Mastermind} \\ $$
Commented by mr W last updated on 06/Jun/22
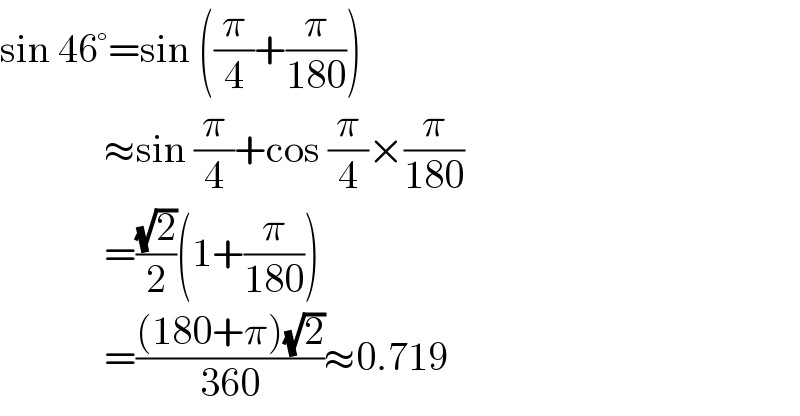
$$\mathrm{sin}\:\mathrm{46}°=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{180}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{sin}\:\frac{\pi}{\mathrm{4}}+\mathrm{cos}\:\frac{\pi}{\mathrm{4}}×\frac{\pi}{\mathrm{180}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+\frac{\pi}{\mathrm{180}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{180}+\pi\right)\sqrt{\mathrm{2}}}{\mathrm{360}}\approx\mathrm{0}.\mathrm{719} \\ $$
