Question Number 146545 by mathdanisur last updated on 13/Jul/21
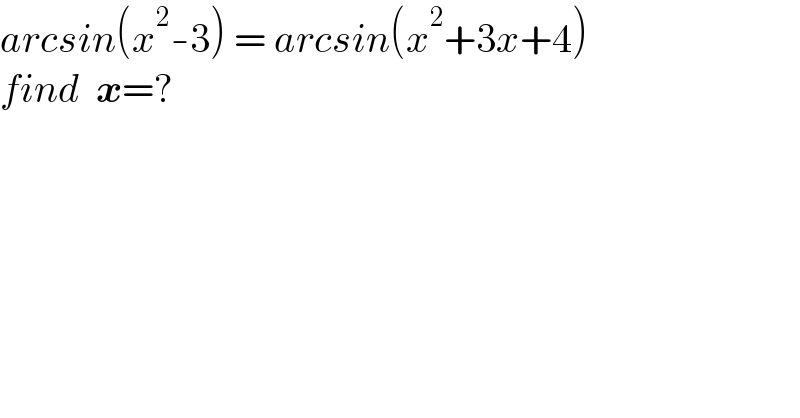
$${arcsin}\left({x}^{\mathrm{2}} -\mathrm{3}\right)\:=\:{arcsin}\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{4}\right) \\ $$$${find}\:\:\boldsymbol{{x}}=? \\ $$
Answered by Olaf_Thorendsen last updated on 14/Jul/21
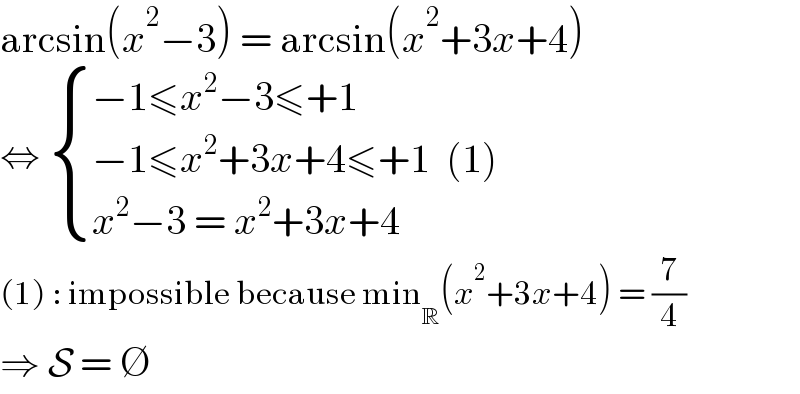
$$\mathrm{arcsin}\left({x}^{\mathrm{2}} −\mathrm{3}\right)\:=\:\mathrm{arcsin}\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{4}\right) \\ $$$$\Leftrightarrow\:\begin{cases}{−\mathrm{1}\leqslant{x}^{\mathrm{2}} −\mathrm{3}\leqslant+\mathrm{1}}\\{−\mathrm{1}\leqslant{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{4}\leqslant+\mathrm{1}\:\:\left(\mathrm{1}\right)}\\{{x}^{\mathrm{2}} −\mathrm{3}\:=\:{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{4}}\end{cases} \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{impossible}\:\mathrm{because}\:\mathrm{min}_{\mathbb{R}} \left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{4}\right)\:=\:\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathcal{S}\:=\:\varnothing \\ $$
Commented by mathdanisur last updated on 14/Jul/21
$${thank}\:{you}\:{Ser}\:{cool} \\ $$
