Question Number 105949 by bachamohamed last updated on 01/Aug/20
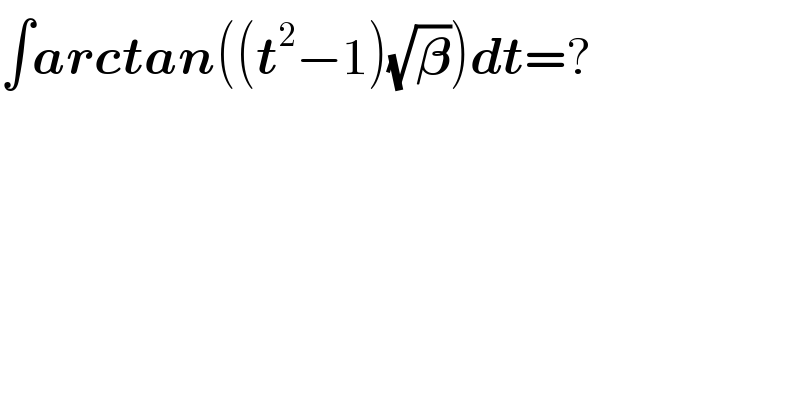
$$\int\boldsymbol{{arctan}}\left(\left(\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\boldsymbol{\beta}}\right)\boldsymbol{{dt}}=? \\ $$
Answered by Her_Majesty last updated on 01/Aug/20
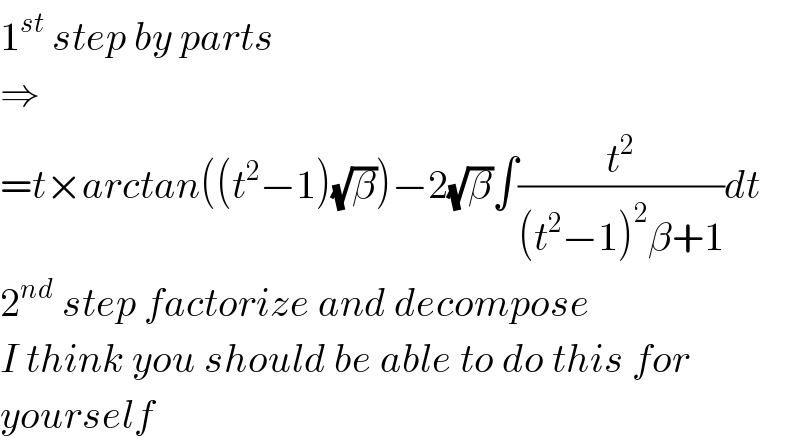
$$\mathrm{1}^{{st}} \:{step}\:{by}\:{parts} \\ $$$$\Rightarrow \\ $$$$={t}×{arctan}\left(\left({t}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\beta}\right)−\mathrm{2}\sqrt{\beta}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \beta+\mathrm{1}}{dt} \\ $$$$\mathrm{2}^{{nd}} \:{step}\:{factorize}\:{and}\:{decompose} \\ $$$${I}\:{think}\:{you}\:{should}\:{be}\:{able}\:{to}\:{do}\:{this}\:{for} \\ $$$${yourself} \\ $$
