arctan-x-x-dx-

Question Number 62908 by aliesam last updated on 26/Jun/19

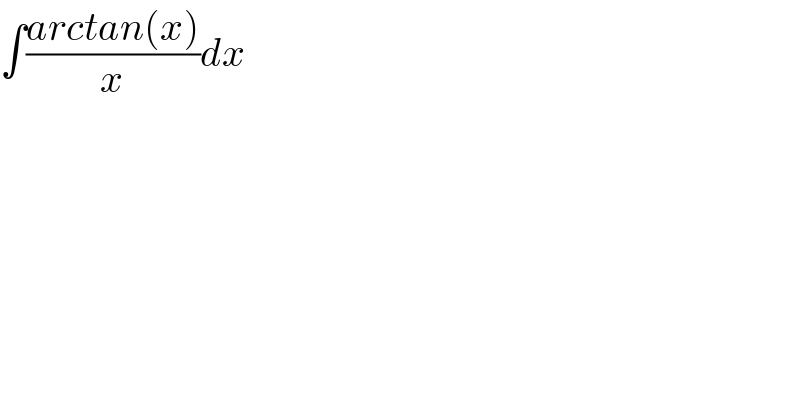
\int \frac{a r c t a n (x)}{x} d x

Commented by mathmax by abdo last updated on 26/Jun/19

f o r a l l x f r o m R u \to \frac{a r c t a n u}{u} i s i n t e g r a b l e o n] 0, x] l e t f (t) = \int_{0}^{x} \frac{a r c t a n (t u)}{u} d u

w e h a v e f^{^{'}} (t) = \int_{0}^{x} a r c t a n (t u) d u =_{b y p a r t s} {[u a r c t a n (t u)]}_{u = 0}^{u = x} - \int_{0}^{x} u \frac{t}{1 + t^{2} u^{2}} d u

= x a r c t a n (t x) - \frac{1}{2 t} \int_{0}^{x} \frac{2 t^{2} u}{1 + t^{2} u^{2}} d u

= x a r c t a n (t x) - \frac{1}{2 t} {[l n (1 + t^{2} u^{2})]}_{u = 0}^{u = x} = x a r c t a n (t x) - \frac{1}{2 t} l n (1 + t^{2} x^{2}) \Rightarrow

f (t) = \int_{0}^{t} x a r c t a n (u x) d u - \int_{0}^{t} \frac{l n (1 + x^{2} u^{2})}{2 u} d u + C \Rightarrow

\int_{0}^{x} \frac{a r c t a n (u)}{u} d u = f (1) = x \int_{0}^{1} a r c t a n (u x) d u - \int_{0}^{1} \frac{l n (1 + x^{2} u^{2})}{2 u} d u + C

x = 0 \Rightarrow C = 0 \Rightarrow \int_{0}^{x} \frac{a r c t a n (u)}{u} d u = x \int_{0}^{1} a r c t a n (u x) d u - \int_{0}^{1} \frac{l n (1 + x^{2} u^{2} 3}{2 u} d u

\dots b e c o n t i n u e d \dots .