Menu Close

Are-they-equal-n-0-sin-n-1-n-1-and-n-1-sin-n-n-

Tinku Tara 0 Comments
Pin




Question Number 121496 by Lordose last updated on 08/Nov/20
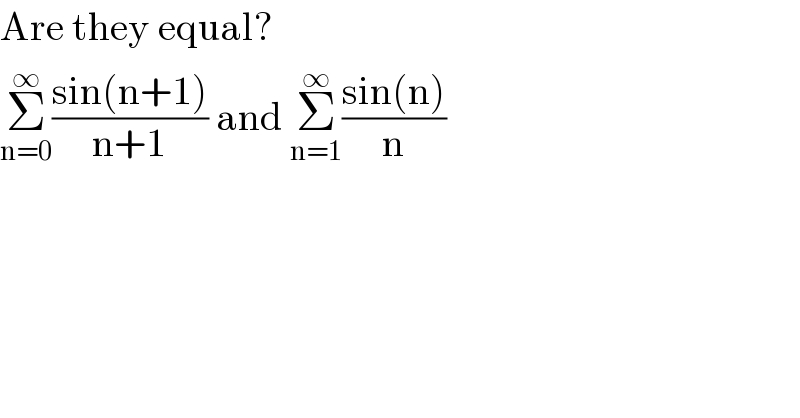
Are they equal? Σ_(n=0) ^∞ ((sin(n+1))/(n+1)) and Σ_(n=1) ^∞ ((sin(n))/n)
$$\mathrm{Are}\:\mathrm{they}\:\mathrm{equal}? \\ $$$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{n}+\mathrm{1}}\:\mathrm{and}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}} \\ $$
Commented by Dwaipayan Shikari last updated on 08/Nov/20
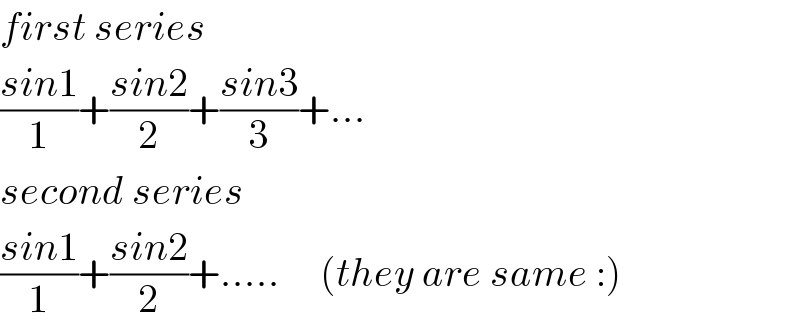
first series ((sin1)/1)+((sin2)/2)+((sin3)/3)+... second series ((sin1)/1)+((sin2)/2)+..... (they are same :)
$${first}\:{series} \\ $$$$\frac{{sin}\mathrm{1}}{\mathrm{1}}+\frac{{sin}\mathrm{2}}{\mathrm{2}}+\frac{{sin}\mathrm{3}}{\mathrm{3}}+… \\ $$$${second}\:{series} \\ $$$$\frac{{sin}\mathrm{1}}{\mathrm{1}}+\frac{{sin}\mathrm{2}}{\mathrm{2}}+…..\:\:\:\:\:\left({they}\:{are}\:{same}\::\right) \\ $$
Answered by TANMAY PANACEA last updated on 09/Nov/20
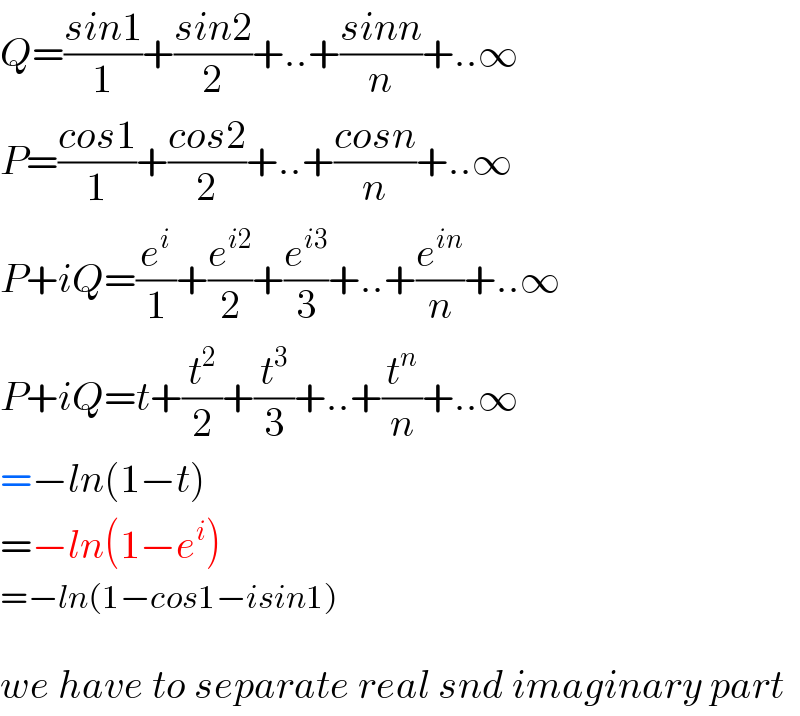
Q=((sin1)/1)+((sin2)/2)+..+((sinn)/n)+..∞ P=((cos1)/1)+((cos2)/2)+..+((cosn)/n)+..∞ P+iQ=(e^i /1)+(e^(i2) /2)+(e^(i3) /3)+..+(e^(in) /n)+..∞ P+iQ=t+(t^2 /2)+(t^3 /3)+..+(t^n /n)+..∞ =−ln(1−t) =−ln(1−e^i ) =−ln(1−cos1−isin1) we have to separate real snd imaginary part
$${Q}=\frac{{sin}\mathrm{1}}{\mathrm{1}}+\frac{{sin}\mathrm{2}}{\mathrm{2}}+..+\frac{{sinn}}{{n}}+..\infty \\ $$$${P}=\frac{{cos}\mathrm{1}}{\mathrm{1}}+\frac{{cos}\mathrm{2}}{\mathrm{2}}+..+\frac{{cosn}}{{n}}+..\infty \\ $$$${P}+{iQ}=\frac{{e}^{{i}} }{\mathrm{1}}+\frac{{e}^{{i}\mathrm{2}} }{\mathrm{2}}+\frac{{e}^{{i}\mathrm{3}} }{\mathrm{3}}+..+\frac{{e}^{{in}} }{{n}}+..\infty \\ $$$${P}+{iQ}={t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+..+\frac{{t}^{{n}} }{{n}}+..\infty \\ $$$$=−{ln}\left(\mathrm{1}−{t}\right) \\ $$$$=−{ln}\left(\mathrm{1}−{e}^{{i}} \right) \\ $$$$=−{ln}\left(\mathrm{1}−{cos}\mathrm{1}−{isin}\mathrm{1}\right) \\ $$$$ \\ $$$${we}\:{have}\:{to}\:{separate}\:{real}\:{snd}\:{imaginary}\:{part} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *